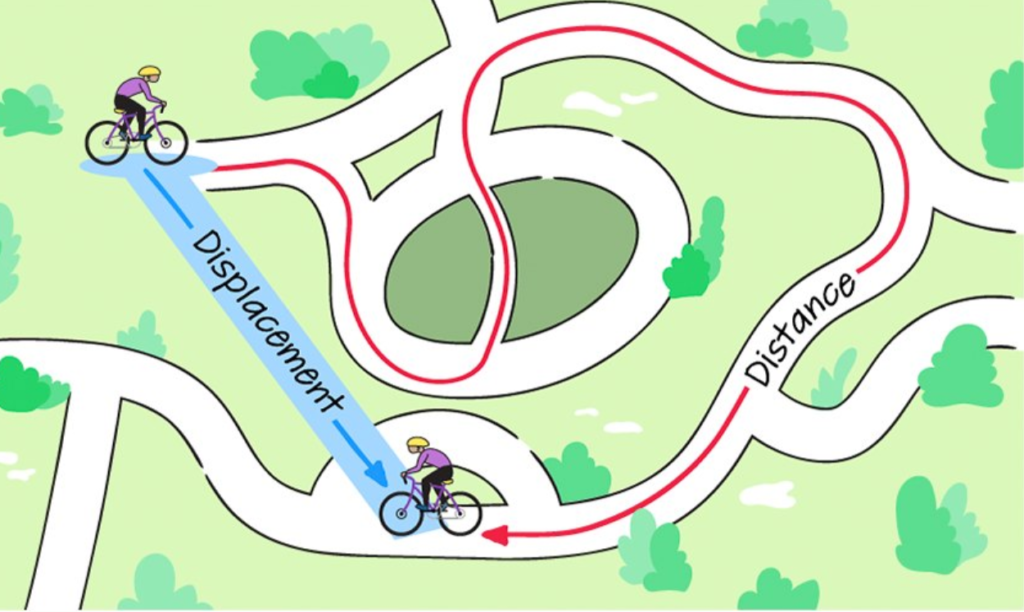
Distance Vs. Displacement, two similar terminologies that should be described and compared precisely. Distance is the real path covered, and displacement is the shortest distance from an origin to a specific destination.
Distance and displacement are two phrases that may seem very familiar and similar to an amateur, but a teacher or student of physics will have a far more prominent meaning of these two terms. Distance and displacement will be two distinct words from English vocabulary for them, but these words will determine a whole new physics concept. Distance and displacement might seem very similar to someone, but both have very different quantities, and both are estimated separately, but they are relevant to each other.
Before further proceeding to the Distance Vs. Displacement topic, we are going to introduce distance and displacement separately.
What Is Distance?
Distance Vs. Displacement should be compared precisely by the definition of each term separately. Distance is a mathematical measurement of how far distant objects or points are. In physics or everyday routine, the distance may indicate a physical length or an estimation based on other standards (e.g., “two counties over”).
The distance between point A to point B is sometimes signified as |AB|. Distance from point A to point B can be readily replaced with distance from point B to point A in most cases. A distance metric or function is a generalization of the notion of physical distance in mathematics; it is a method of explaining what it means for components of some space to be “far apart from” or “close to” each other.
In social sciences and psychology, distance is a non-numerical quantity; Psychological distance is designated as “the diverse ways in which an object might be eliminated from” the self along dimensions such as “social distance, time, space, and hypotheticality.
With the aid of an example, the concept of distance can be explained better. For instance, you leave your office and travel five meters north, retake a right, walk five meters, repeatedly take a right and walk five meters and again take a right and walk five meters. You will end up in the same place; still, the distance you have traveled is 20 meters.
Physical Distances
A physical distance can express various things:
- Distance traveled: The length of a particular path moved between two points, such as the distance hiked while piloting a maze
- Straight-line distance: The length of the shortest feasible path within space, among two points, that could be considered if there were no barriers
- Geodesic distance: The the shortest path length among two points while prevailing on some surface, such as the great-circle distance along the Earth curve
A specific path’s length returns to the origin point, such as a ball thrown straight up or the Earth when it finishes one orbit.
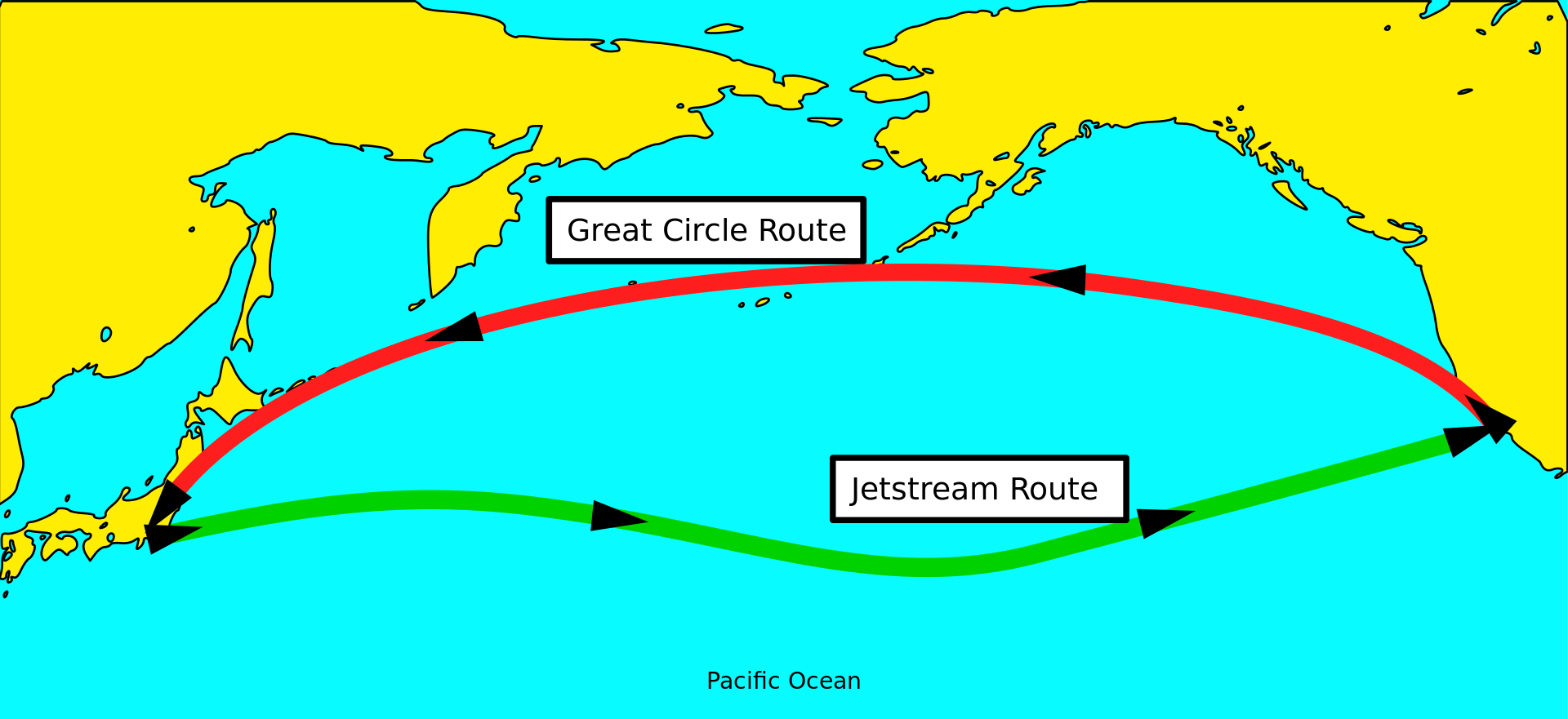
Theoretical Distances
The term “distance” is also employed by analogy to measure non-physical entities in specific ways.
In computer science, an idea exists that tells about the “edit distance” among two strings. For instance, the words “dog” and “dot”, which differ by only one letter, are more intimate than “dog” and “cat”, which vary by three letters. This idea is applied in spell checkers and coding theory and is mathematically formalized in numerous distinct ways such as:
In mathematics, a metric space is a collection for which distances among all set members are described. In this way, several kinds of “distances” can be determined, such as traversing graphs, comparing patterns and curves, and applying unusual interpretations of “space”. The concept of distance in graph theory has been adopted to describe social networks.
In psychology, social sciences, and human geography, distance is frequently theorized not as an objective metric but as a subjective reality.
What Is Displacement?
Displacement is truly the distance a soul is away from its original point or the origin point. In other words, it is the distance between you and the origin point. Displacement informs you how far you are actually from the origin point. It can be explained better with the subsequent example.
If you have your notebook in your bag and leave home and walk five meters north and reach your office, then the displacement between you and your book will be zero since you did not move away from your notebook.
Distance Vs. Displacement
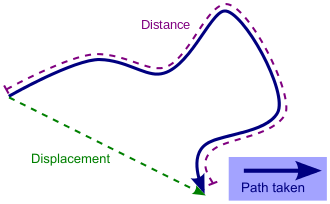
Here is the basic description of Distance Vs. Displacement: Distance is the measure of how far away you have traveled so far, whereas displacement designates how far you are away from the origin point irrespective of the space you have covered.
Displacement does not include the steps taken, or the area met while traveling. It merely determines the distance from the point you are and the point you originally began from. This is while distance measures and calculates every area covered even though the area might be included twice by the object, and it determines the total area or path covered entirety.
One of the most notable distinctions between Distance Vs. Displacement is that the distance covered among the two points is regularly bigger or equal to the magnitude of displacement.
Another difference between Distance Vs. Displacement is that distance is estimated even in curves, while displacement is in a straight line. Distance is the real path covered, and displacement is the shortest distance from the object to the point of origin.
Both distance and displacement measure the displacement of an object. The distance cannot be negative and never diminishes. Distance is a magnitude or scalar quantity, while displacement is a vector quantity including both magnitude and direction. It can be negative, zero, or positive. Directed distance does not include movement; it measures the separation of two points and can be a positive, zero, or negative vector.
Here is a comprehensive video representing fundamental differences between Distance Vs. Displacement.
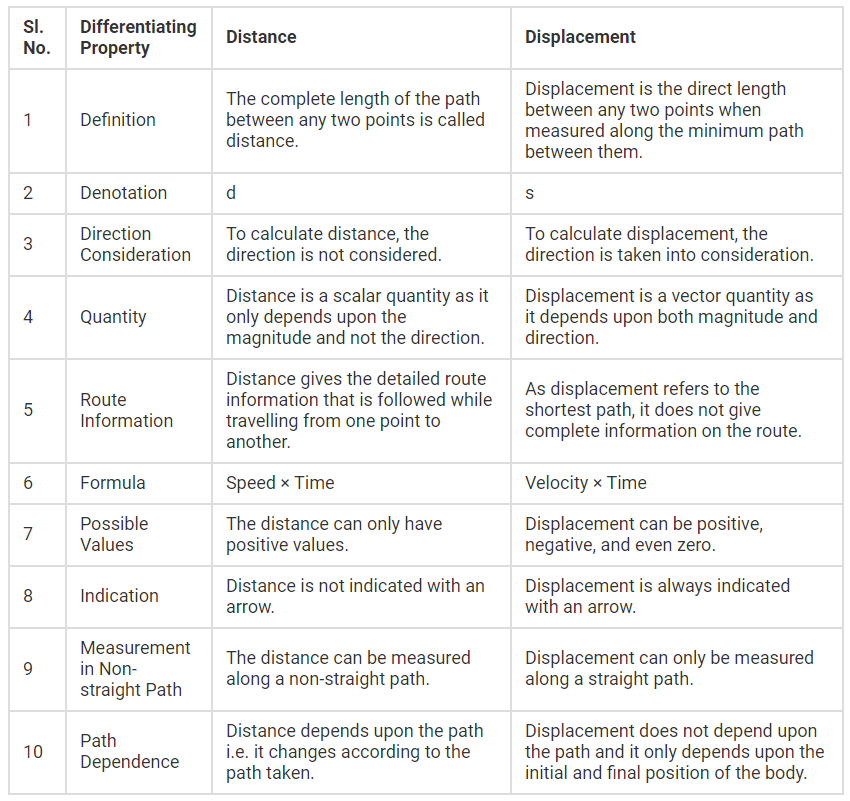
Comparison Chart
Here we propose a summarized table indicating the main Distance vs. Displacement differences:
Mathematics
Here we introduce some formulas to determine Distance Vs. Displacement topic more accurately.
Geometry
In analytic geometry, the Euclidean distance within two points of the XY-plane can be determined using the distance formula. The distance between (x1, y1) and (x2, y2) is provided by:
d=\sqrt { { (\Delta x) }^{ 2 }+{ (\Delta y) }^{ 2 } } =\sqrt { { ({ x }_{ 2 }-{ x }_{ 1 }) }^{ 2 }+{ ({ y }_{ 2 }-y_{ 1 }) }^{ 2 } }
Likewise, given points (x1, y1, z1) and (x2, y2, z2) in three-dimensional space, the distance between them is:
d=\sqrt { { (\Delta x) }^{ 2 }+{ (\Delta y) }^{ 2 } +{ (\Delta z) }^{ 2 }} =\sqrt { { ({ x }_{ 2 }-{ x }_{ 1 }) }^{ 2 }+{ ({ y }_{ 2 }-y_{ 1 }) }^{ 2 }+{ ({ z }_{ 2 }-{ z }_{ 1 }) }^{ 2 } }
These formulas are readily determined by constructing a right triangle with a leg on another’s hypotenuse and employing the Pythagorean theorem. This distance formula can also be extended into the arc-length formula. Other distances with other formulas are applied in Non-Euclidean geometry.
Distance in Euclidean Space
In the Euclidean space Rn, the interval between two points is typically given by the Euclidean distance. Other distances, based on different norms, are sometimes employed instead.
For a point (x1, x2, …, xn) and an end (y1, y2, …, yn), the Minkowski distance of order p (p-norm distance) is determined as:
One – norm distance = \sum _{ i=1 }^{ n }{ \left| { x }_{ i }-{ y }_{ i } \right| }
Two– norm distance = { \left( \sum _{ i=1 }^{ n }{ { \left| { x }_{ i }-y_{ i } \right| }^{ 2 } } \right) }^{ 1/2 }
p – norm distance = { \left( \sum _{ i=1 }^{ n }{ { \left| { x }_{ i }-y_{ i } \right| }^{ p } } \right) }^{ 1/p }
Infinity norm distance = { \lim _{ p\rightarrow \infty }{ \left( \sum _{ i=1 }^{ n }{ { \left| { x }_{ i }-y_{ i } \right| }^{ p } } \right) } }^{ 1/p } =max(\left| { x }_{ 1 }-y_{ 1 } \right| ,\left| { x }_{ 2 }-y_{ 2 } \right| ,...,\left| { x }_{ n }-y_{ n } \right| )
p must not be an integer, but it cannot be smaller than 1; otherwise, the triangle inequality does not sustain.
The 2-norm distance is the Euclidean distance, a generalization of the Pythagorean theorem to more than two coordinates. It would be obtained if the distance between two points was estimated with a ruler: the “intuitive” idea of distance.
The 1-norm distance is more colorfully named the taxicab norm or Manhattan distance since it is the distance a car drive in a city laid out in square blocks.
The infinity norm distance is also termed Chebyshev distance. In 2D, the minimum number of moves kings need to travel between two squares on a chessboard.
The p-norm is infrequently used for p other than 1, 2, and infinity values.
In physical space, the Euclidean distance is the most reasonable one, because in this case, the length of a rigid body does not vary with rotation.
Conclusion
Distance and displacement are two distinct yet linked terminologies regularly used in physics. Distance and displacement are indeed the paths covered irrespective of the direction; they are just involved with the quantity of the path covered.