Difference between Electric and Magnetic Fields – The attraction and repulsion of electric charges result in both electric and magnetic fields. However, a magnetic effect is created around a permanent magnetic object or caused by moving electric charges, whereas an electric field originates from stationary charges, or wherever a voltage is present. The interaction of electric and magnetic fields is what permits occurrence of electromagnetic waves, such as heat and light. This relevance is essential for the universe to function as it does now.
Electric Field
What Is Electric Field?
Electric fields are formed around every particle in space that carries any type of electric charge. The value of E, also known as electric field strength, electric field intensity, or simply the electric field, expresses the magnitude and direction of the electric field. Rather than thinking of the electric force as a direct interaction between two electric charges at a distance, one charge is assumed of as the source of an electric field that spreads out into the surrounding space and the force applied on a second charge in this space is thought of as a direct interaction between the electric field and the second charge.
The electric force F applied per unit positive charge electric q at any place defines the strength of an electric field E at that point:
\vec{E}= \frac{\vec{F}}{q}
The resulting force is doubled if the second, or test, charge is twice as large; nonetheless, their quotient, the magnitude of the electric field E, remains constant at any given point. The source charge, not the test charge, determines the strength of the electric field. The strength of an electric field is measured in Newton per Coulomb (N/C); although the derived SI units of volts per meter (V/m) are more commonly used for the electric field that is equivalent to Newton per Coulomb.
Coulomb’s Law
Coulomb’s Law can be utilized to compute the electric field. According to this law, the electric force between two point charges is directly proportional to the charge product and is inversely proportional to the square of the distance of separation between them:
F= \frac{q_{1}q_{2}}{4\pi \varepsilon_{0} r^{2}}
Where, q1 and q2 are the values of the two charges, ε0 is permittivity of vacuum (which is equal to 8.85 ×10-12 C2N-1m-2 or epsilon naught value) and r is distance between the charges. The electric field is described as the force per unit charge; hence, q1 = q and q2 = 1. The electric field is then calculated with regard to the equation below:
E= \frac{q}{{4\pi \varepsilon_{0} r^{2}}}
As a result, the quantity of the source charge determines the strength of an electric field. The nature of the medium plays a major role as well. The electric field is always reduced in the presence of a material medium below its value in a free space.
The strength of an electric field at any point is equal to the vector sum of all electric fields operating at that point:
\vec{E}= \vec{E_{1}}+\vec{E_{2}}+...+\vec{E_{n}}= \frac{\vec{F_{1}}}{q_{1}}+\frac{\vec{F_{2}}}{q_{2}}+...+\frac{\vec{F_{n}}}{q_{n}}= (\frac{1}{4\pi \varepsilon _{0}})(\frac{q_{1}}{r_{1}^{2}})+ (\frac{q_{2}}{r_{2}^{2}})+...(\frac{q_{n}}{r_{n}^{2}})
Electric Field Lines
Electric field lines are an effective approach to visualize electric fields. These lines, which are formed by a vector field and a beginning location inside the field, serve as a kind of map that provides information about the direction and strength of the electric field at different points in space.
Direction of Electric Field
The field’s direction is considered as the direction of the force it would apply on a positive charge. The electric field around a single positive charge is directed radially outward because positive charges repel each other. The force acting on a negative charge is directed in the opposite direction as the force exerted on a positive charge. Therefore, the electric field is directed radially in toward a single negative charge. For an isolated electrical charge, electric field lines originate from a positive charge and continue out to infinity, or they come in from infinity and terminate on negative point charge. Electric fields are illustrated as starting on positive charges and ending on negative charges when represented by field lines.
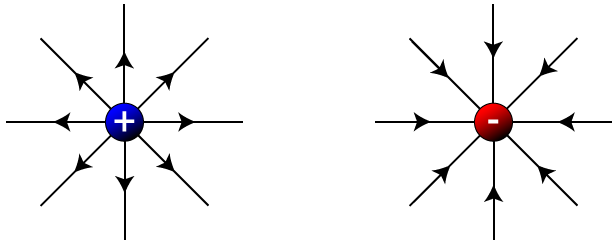
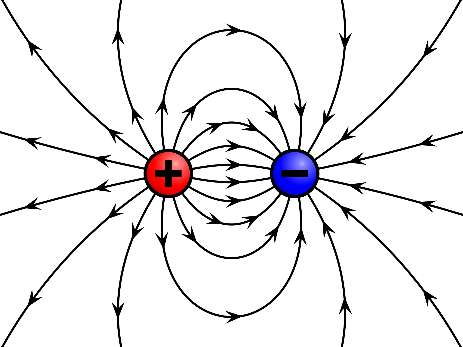
It’s important to remember that lines can’t cross one another. Since a field line specifies the direction of the field at a particular point, crossing two field lines at a single point implies that the electric field is pointing in two separate directions. As a consequence, the net force acting on a test charge positioned at that location would point in different directions. As this is clearly impossible, field lines must never intersect. Since the electric field is conservative in nature, it never makes a closed loop. The direction of the electric field at a point is represented by a line tangent to a field line at that point.
Magnitude of Electric Field
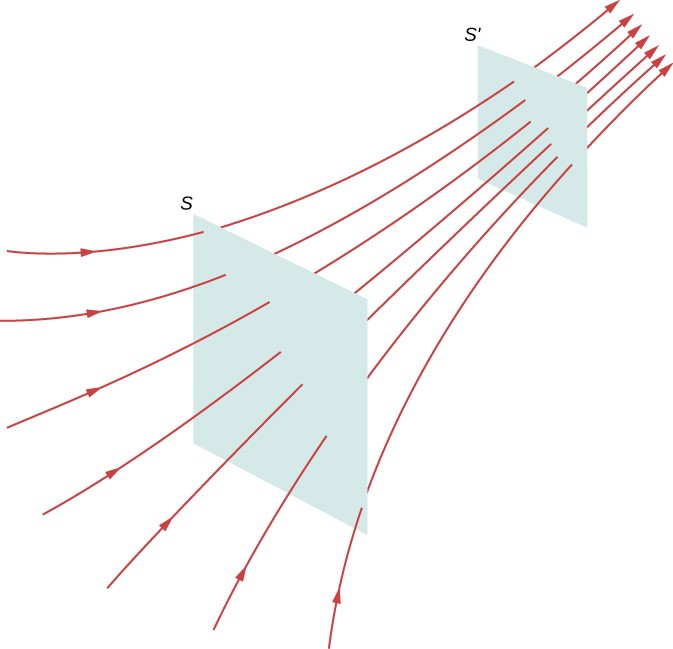
The field line density, or the number of field lines per unit area flowing through a short cross-sectional area perpendicular to the electric field, indicates the magnitude of the field. The density of the field line at that cross-section is drawn to be proportional to the magnitude of the field there. Hence, if the field lines are near together (i.e., the field line density is more), it implies that the magnitude of the field is great at that point. When the field lines in a cross-section are widely apart, the magnitude of the field is modest.
In the following figure, both surfaces (S and S’) have the same number of field lines passing through them, but surface S’ is smaller than surface S. As a result, the density of field lines is higher at S’ than at S, implying that the electric field is greater at S’ than at S.
Read More on Linquip
- Difference Between Energy and Power
- What is the Difference Between Oscillator and Crystal?
- A Simple Guide to the Difference Between Motor and Generator
- Difference Between Scalar and Vector Quantity
Magnetic Field
What is Magnetic Field
A magnetic field is formed around a permanent magnetic substance or when an electrically charged object moves. The pole of a magnet, a current-carrying wire or a moving charged particle in a magnetic field feel a magnetic force. The magnetic flux density B, or simply the magnetic field, represents the strength of the magnetic field. In electric fields, the field’s direction is in direction of the force exerted on a positive charge. Similarly, the direction of magnetic flux density corresponds to the direction of force on an isolated North Pole.
The magnetic force exerted on a wire carrying current I with length L in a magnetic field is given by the following equation:
\vec{F}= L \vec{I}\times \vec{B}= LIBsin(\theta )
Where “×” denotes the cross product and θ is the angle between the wire and the magnetic field. As the cross product of two vectors is perpendicular to each of the two vectors, the magnetic field’s force is perpendicular to both the direction of current and the direction of the magnetic field.
The next equation is the corresponding formula for the force on a moving charged particle with charge q and velocity v:
\vec{F}= q \vec{v}\times \vec{B}= qvBsin(\theta ))
Where θ is the angle made between the particle velocity and the magnetic field, and the force is perpendicular to the field and the motion direction. B has units of (Newton. Second)/ (Coulomb. meter), (N.s)/ (C.m), according to both equations (5) and (6). Tesla (T), which is equal to 104 gauss (G), is the name given to this combination of units in SI.
Because we commonly find ourselves integrating B over a mathematical surface in engineering electromagnetics, we prefer to refer to B as a “flux” density. The term “flux” refers to any quantity obtained by integrating over a surface. Therefore, it’s normal to conceive B as a flux density, or flux F per unit surface area A. The weber is the SI unit for magnetic flux (Wb). As a result, B can also be written as the following equation with Wb/m2 unit; hence 1 Wb/m2 equals 1 T.
\vec{\phi }= \vec{B}.\vec{A}= BAcos(\theta )
Where θ is the magnetic field’s angle with the area. As a result, the field strength, B, is equal to F/A, where A is the area perpendicular to the magnetic field B.
Ampere’s Law
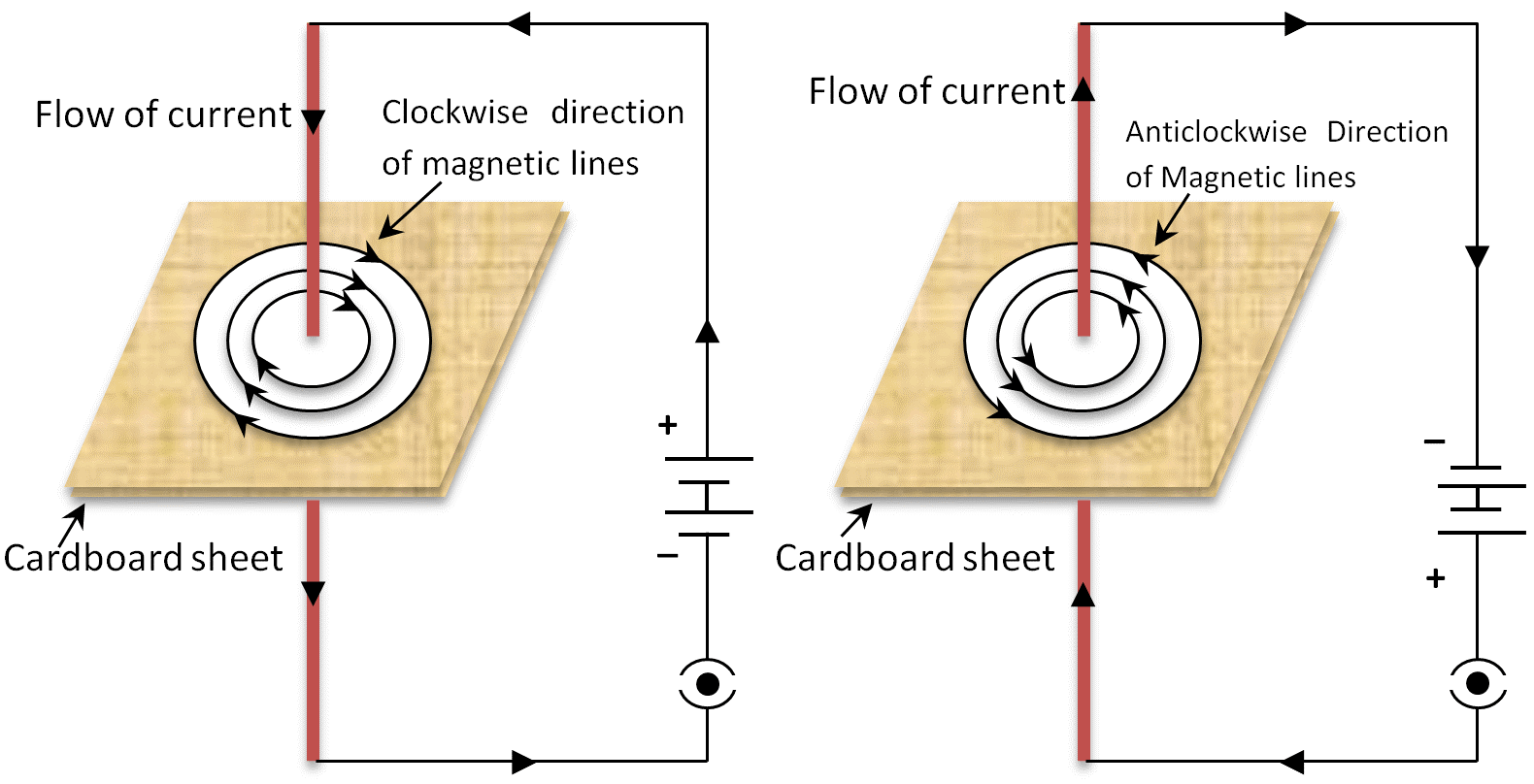
Currents generate magnetic fields, according to Ampere’s Law, or in other words, wherever there is a current flow, a magnetic field circulates around it. The field grows proportionally when the current (amount of charge in motion) is increased. As we get further away from the wire, the strength of the field decreases accordingly. This is described by Ampere’s law; the magnetic field at a distance r from a long straight wire carrying current I (passing through that path) is calculated by:
B= \frac{\mu_{0} I}{2\pi r}
Where μ0 is the permeability of free space, which has a constant value of μ0=4π×10−7 T⋅m/A. The direction of the magnetic field is specified via the right-hand-grip rule. To use this rule, wrap your right hand around the wire with your thumb pointing in the current’s direction. The fingers show the direction of the magnetic field that wraps around the wire.
Magnetic Field Lines
The usage of field lines is an efficient approach to express the information contained within a vector field. These lines aren’t real, but they’re an excellent way to visualize some of magnetism’s features.
Direction of Magnetic Field
There is always one north and one South Pole on a magnet. The magnetic field is a vector field, with magnitude and direction at each point. The force that the north pole of a magnet would receive at that point is defined as the direction of the force. Because like poles repel and opposing poles attract each other, the magnetic field of a magnet moves away from its North Pole towards its South Pole. The field vector at any location in space is tangent to the field line at that same place.
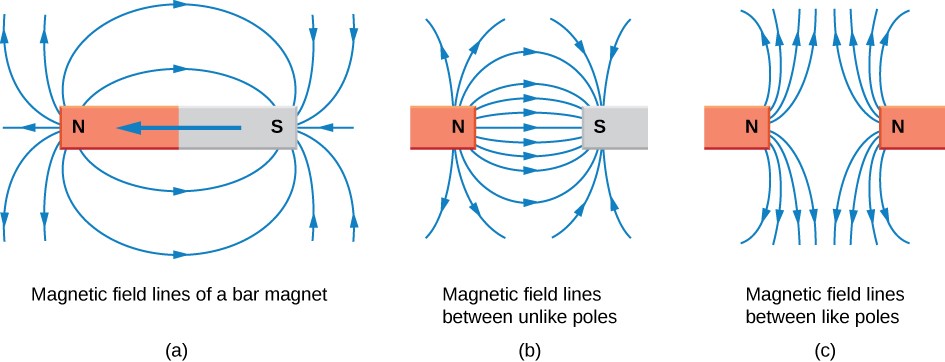
Magnetic field lines can never cross, implying that each point in space has a unique field. They also don’t start or stop somewhere; instead, they always form closed loops and will continue to do so within a magnetic material.
Magnitude of Magnetic Field
Like electric field lines, magnetic field lines naturally cluster in areas where the magnetic field is most potent. It means that the density of field lines reflects the field’s strength. The field’s magnitude is proportional to the closeness of the lines. It is proportionate to the number of lines per unit area perpendicular to the lines. As a result, the magnetic field is stronger when the lines are closer together.
You can also find more details about magnetic fields in our other posts.
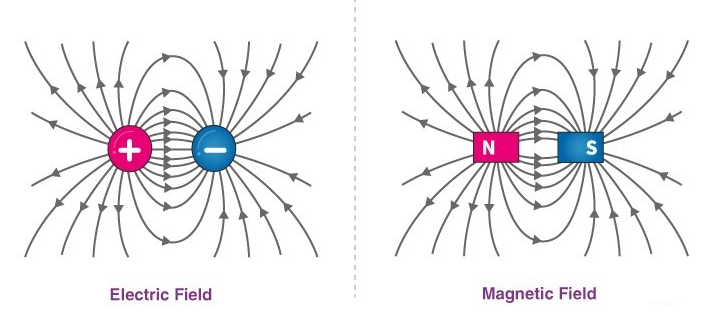
What Are Difference between Electric and Magnetic Fields
The nature of the magnetic and electric fields differs in that the electric field is induced around a static electrically charged particle that is either positive or negative; whereas the magnetic field is created around the poles (i.e., the north and south poles) of a permanent magnet substance or a moving electrically charged object. Some other differences between them are explained as below:
- Unit: The electric field is measured as Newton per Coulomb (N/c), or Volt per Meter (V/m). In comparison, the strength of the magnetic field is represented by either Tesla (T) (equal to (Newton × Second) / (Coulomb × Meter)) or Wb/m2.
- Force: The electric field is expressed as the force per unit charge experienced by a stationary point charge at any given place inside the field, whereas the magnetic field is defined as the force exerted on other magnetic particles and moving electric charges.
- Field line: In an electric field, field lines are induced on a positive charge and terminate on a negative charge, but they do not form a closed loop; however, in a magnetic field, field lines are generated at the North Pole and terminate at the South Pole, and they continue inside a magnetic material and form a closed loop.
- Symbol: The electric field intensity is expressed by the symbol E whereas the magnetic field intensity is expressed by B.
- Formula: The magnitude of an electric field is calculated with the formula E=F/q Newton/Coulomb. The magnetic field is calculated with B=F/A tesla or Wb/m2.
- Measuring instrument: An electrometer measures the electric field intensity, whereas a magnetometer measures the magnetic field intensity.
- Pole: An electric field is produced by a unit pole charge, which can be either positive or negative, whereas a magnetic field is produced by a dipole of a magnet (i.e., the north and South Pole).
- Electromagnetic field: Both electric and magnetic fields are components of an electromagnetic field that occupy different planes in relation to the electromagnetic field’s cause, such as a moving electrical charge. The directions in which the electric and magnetic fields flow in an electromagnetic field are perpendicular to one other.
- Work: The electric field has the ability to work. When a particle encounters an electric field, it can be influenced by the electric field, which can change the particle’s velocity and direction. The magnetic field is incapable of doing any work. When a particle enters the field of influence of a magnet, the magnet field has no effect on the particle’s velocity or direction.



i do not understand can you please clarify