Difference Between Energy and Power: 2021 Practical Guide

Table of Contents

Difference Between Energy and Power – Energy, to express it as simply as possible, is the ability to work. Work is defined as the act of exerting a force over a distance in physics. Power determines the rate at which energy is produced or consumed, i.e. energy per unit of time. While energy measures the overall amount of work done, power refers to how quickly the work may be completed.

Energy

What Is Energy?

Energy is the quantifiable attribute that must be supplied to a body or physical system for work to be done. In other terms, energy is defined as the ability to perform work. The joule, abbreviated J, is the unit of energy measurement in the International System of Units (SI). In mechanics, one joule is the amount of energy transmitted when a force of one Newton (N) is applied to an object, and it is moved over a distance of one meter (m). Hence, the general formula for calculating the amount of work that is done on an object is:

$W=\int_{c}^{}F\cdot dS$

The work, represented by W, is equal to the line integral of the force F along a route C; therefore, work, and consequently energy, is dependent on the frame. The simplest expression of the above formula is as follows:

$W=\vec{F}\cdot\vec{S}= FScos(\theta )$

Where θ is the angle formed by the vectors of force (F) and displacement (S). The important point here is that only the component of the force that is parallel to the displacement, F∣∣, conducts work on an item.

A calorie is another type of energy unit. Calories are commonly used to express the quantity of energy in a food item. The amount of energy required to heat 1 kilogram of water by 1 degree Celsius is one calorie. This corresponds to 4184 joules per calorie.

Conservation of Energy

The law of energy conservation, sometimes known as the first law of thermodynamics, holds that energy can be transformed but cannot be generated or destroyed. Hence, the energy is considered as a conserved quantity. This, in the form of the first law of thermodynamics, explains that when energy passes into or out of a system (in the form of work, heat, or matter), the system’s internal energy varies in accord with the law of conservation of energy. Total energy intake into a system must equal total energy output plus the change in the energy contained within the system.

Energy Transfer

There are three types of systems in thermodynamics in terms of energy transfer: open, closed, and isolated, which are described below.

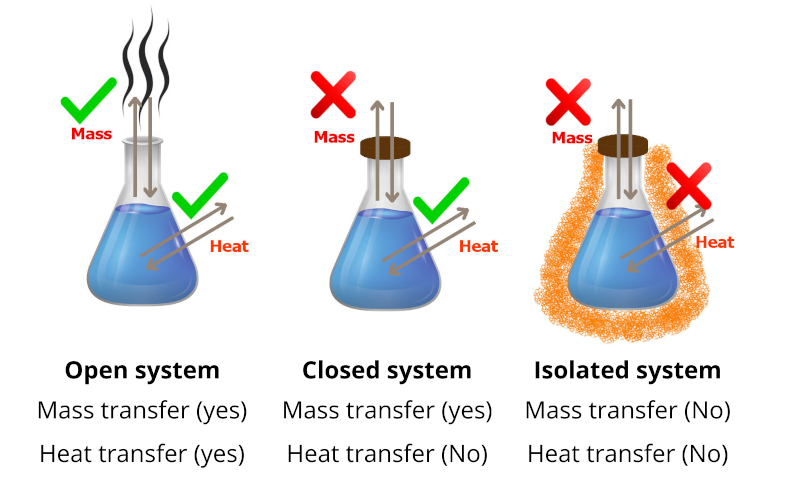
Difference Between Energy and Power — Energy transfer in different types of thermodynamic systems (Reference: **lawofthermodynamicsinfo.com**)

Isolated System

An isolated system is a thermodynamic system that cannot exchange either energy or matter outside the boundaries of the system. A good example of an isolated system is the thermos flask.

$\Delta E = 0$

Closed System

A closed thermodynamic system can exchange energy (as heat or work) but not matter with its surroundings. Regarding to the first law of thermodynamics, the energy for such a system is constant until energy is transported in or out by work or heat, and that no energy is wasted in transmission.

$\Delta E = W + Q$

Where E E {\displaystyle E} is the quantity of energy transferred, and consequently, ΔE expresses changes in internal energy, W {\displaystyle W} W shows the work done on the system, and Q Q {\displaystyle Q} represents the heat flow into the system.

Open System

Open systems can lose or gain energy in conjunction with matter transfer, which is beyond the restrictions of closed systems; Denoting this energy by E for an open system, the first law of thermodynamics can be written:

$\Delta E = W + Q + E$

Forms of Energy

Energy can neither be created nor destroyed. It is just transformed from one form to another, working in the process. Energy can be stored and measured in many forms, such as electrical energy, thermal energy, radiant energy, nuclear energy, and chemical energy, as Figure below. (a) Thermal energy is produced by atomic and molecular motion; molten steel at 2000°C has a very high thermal energy output. (b) Radiant energy (from the sun, for example) is the energy contained in light, radio waves, and microwaves. (c) Lightning is an instance of electrical energy that occurs due to the movement of particles that bear electrical charges. (d) Nuclear energy is released as the particles in the atom’s nucleus are rearranged. (e) Chemical energy is generated by the arrangement of atoms in a chemical compound; heat and light are produced as a result of energy released during the breaking and reforming of chemical bonds.

For instance, chemical energy is contained in food, and this energy is stored in the body until it is used as kinetic energy during activity. When a box slides down a hill, the potential energy that the box possesses as a result of its location high up on the slope is transformed into kinetic energy or energy of motion. As the box comes to a halt due to friction, the kinetic energy from its motion is turned to thermal energy, which heats both the box and the slope.

The total forms of energy in a system can be grouped into two general types of macroscopic energy for conducting work:

Potential or stored energy;
Kinetic or working energy;
Combinations of the above items.

Potential Energy

The potential energy, U, indicates the potential of an object to move and is commonly defined as the stored energy held by a system due to the relative positions or orientations of its components subjected to a conservative force. Electrical energy, nuclear energy, and chemical energy are different forms of potential energy. If F and x represent the conservative force and the position, respectively, the potential energy of the object subjected to the force between the two positions x₁ and x₂ is determined as the negative integral of F from x₁ to x₂:

$U = -\int_{x1}^{x2}F\cdot dx$

Kinetic Energy

The kinetic energy, K, of an object relies on its speed and is the capability of a moving object to do work on other objects when they crash. It is calculated as one-half the product of a mass of an object, m, divided by its speed, V, squared, and the total kinetic energy of a system of elements is the sum of the kinetic energies of the separate elements.

$K = \frac{1}{2}mV ^{2}$

Macroscopic Mechanical Energy

While the two above-mentioned categories are appropriate for describing all forms of energy, it is often more practical to refer to specific combinations of potential and kinetic energy as a separate types. Macroscopic mechanical energy, E, for example, is the total of a system’s potential and kinetic energy:

$E_{mechanical}= U + K$

The principle of mechanical energy conservation holds that if an isolated system is only subjected to conservative forces, the mechanical energy will remain constant. A conservative force differs from a non-conservative force in that when a conservative force moves an object from one place to another, the work done on the object is independent of the path. When a non-conservative force operates on an item, the work done is dependent on the path taken by the non-conservative force. Non-conservative forces, such as frictional forces, will be present in all practical systems, but if they are small, the mechanical energy changes little and its conservation is a reasonable assumption.

Power

What Is Power?

The rate at which work is done or energy is transmitted or converted, is measured in power, P. In other words, it is the time derivative of work. Power is taken as the scalar quantity. The Watt, abbreviated W, is the standard unit for measuring power. A watt is described as one joule of work done per second.

$P = \frac{dW}{dt}$

If the work done by a force, F, is substituted into the above equation, it can be expressed as below, considering V as the velocity of an object caused by the force applied.

$P = \frac{dW}{dt}=\frac{d(\int_{c}^{}F\cdot dS)}{dt}= \frac{d(\int_{\Delta t}^{}F\cdot \frac{ds}{dt}dt)}{dt}= \frac{d(\int_{\Delta t}^{}F\cdot Vdt)}{dt}= \vec{F}\cdot \vec{V}$

Horsepower is also another unit that describes the power delivered by a machine. This is commonly denoted by the symbol hp and is defined as the force necessary to lift a 75 kg load one meter in one second. One mechanical horsepower is equivalent to 735.5 watts (g = 9.807 m/s²).

Average Power

If P_avg represents average power in watts, ΔE is the change in energy, and ΔW is the amount of work done during a period of Δt, the following equation is used to compute it:

$P _{avg}= \frac{\Delta E_{sys}}{\Delta t}= \frac{\Delta W}{\Delta t}$

The limiting value of the P_avg is the instantaneous power as the time interval Δt approaches zero.

$P = \lim_{\Delta t\rightarrow 0}P_{avg}= \frac{dW}{dt}$

The value of work done over some time t in the situation of constant power P is given by:

$W=Pt$

This is why a kilowatt is a power unit, whereas a kilowatt-hour (1-kilowatt times 1 hour) is an energy unit.

Difference between Energy and Power

Energy and power are not the same physical quantity although they are closely related. Energy is concerned with the amount of work that can be done using force, whereas power points to the rate at which work is done.

For example, capacitors typically have a small amount of energy that can be quickly discharged. Because of the short duration, they can have a lot of power even if they just have a small amount of stored energy. Batteries, on the other hand, hold a lot more energy than a capacitor but release it much more slowly, resulting in lower power output. Similarly, lifting a box takes a certain amount of energy, regardless of how rapidly it is taken up. Lifting more quickly will increase the amount of power but not the amount of energy required.

Some other differences between energy and power are explained below:

Definition: The ability to work is defined as energy. In comparison, power is the rate at which energy is transmitted or work is done. Energy is power integrated through time.
Transformation: A wide variety of devices can be employed to convert one form of energy into another. For example, an electric bulb converts electrical energy into light and heat, or a battery converts chemicals to electric energy. Power cannot be converted or transformed.
Unit: Energy is measured as Joule (J), which is equal to Watt × Seconds (W.s) or Newton × Meter (N.m). The other measurement units include calories and ergs. Power is represented by Watt that is corresponded to Joule per Second (J/s).
Symbol: Energy is denoted by the symbol E, or sometimes W for the work done, whereas power is expressed by P.
Formula: Power is described as the rate of change of energy of a subsystem or the work done: P = Wt, where W is work, t is time, and P is power.
Measuring instrument: Although energy cannot be directly measured, the work performed can be specified and measured. A thermometer, which measures temperature, a calorimeter, which measures the heat received or released in chemical processes or physical changes, or a bolometer, which measures the intensity of radiation, are all used for this purpose. Power cannot be stored, but energy can. Because power is defined as energy per unit of time, it may theoretically be determined by measuring the amount of energy utilized per second.