Now, we want to talk about the difference between scalar and vector quantity. Every scientific explanation can be described with the help of different physical quantities; each expresses a special meaning and importance in that context. Based on the definition, a physical quantity is the quantifiable and measurable physical property that carries unique information. Based on their dependency on the direction, physical quantities can be divided into two categories — scalar and vector. Both of these quantities are in practice to represent the motion of an object. Let us now explain what the difference between scalar and vector quantity is.
Scalar Quantity
A scalar quantity is a type of quantity that has just magnitude and no direction. Therefore, it is simply a number accompanied by an identical unit. For example, length, mass, speed, duration, etc., are scalars; hence they have no direction. A scalar quantity has no specific direction of application; its value will be precisely the same in every direction.
The value of the scalar will be precisely the same in all directions. Therefore, every scalar is a one-dimensional parameter. As a result, any change in scalar quantity reflects only a difference in magnitude, as no direction is connected with it.
The rules of ordinary algebra can be utilized for calculating scalar quantities. For instance, scalars can be added, subtracted, or multiplied, in the same way, as numbers. Just keep in mind that the operation of the scalar quantities with the same measurement unit is possible. The multiplication of two scalar quantities is identified as the dot product.
What We Should Know About Scalar Quantity
- Scalar quantity indicates that the physical quantity has only magnitude and no direction.
- Any difference in scalar quantity indicates only a difference in the magnitude of the concerned physical amount.
- Scalar quantities are regularly one dimensional.
4.A scalar quantity can divide another non-zero scalar quantity.
- Scalar quantity matches the ordinary rules of algebra. Consequently, a usual algebraic method can be applied to solve scalar quantities.
- Any mathematical calculation/operation among two or more scalar quantities will continuously result in a scalar quantity.
- Any mathematical calculation between a scalar quantity and a vector quantity will always end in a vector quantity.
- Scalar quantities cannot be resolved; it has precisely the same value in all directions.
Examples of Scalar Quantity
Some examples of scalar quantities are presented here.
- Speed
- Work
- Distance
- Power
- Temperature
- Volume
- Charge
- Gravitational potential
- Frequency
- Energy
- Length
- Kinetic energy
- Specific heat
- Power
- Calorie
- Density
- Entropy
Vector Quantity
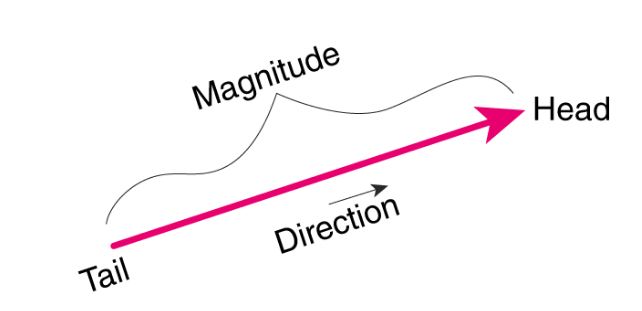
A vector quantity has magnitude with the unit and a particular direction. So specifying the direction of action and its value or magnitude is obligatory while defining or stating a vector quantity.
In a vector quantity, magnitude represents the size of the quantity, which is also its total value, while direction describes the side, i.e. west, east, north, south, etc. We represent vector quantities in either of the parameters, i.e. one-dimensional, two-dimensional, or three-dimensional parameters. Any change in the vector quantity reflects either magnitude shift, change in direction, or change in both of them.
One can resolve vector quantity with the help of sine or cosine of adjacent angles (vector resolution). A vector quantity always follows the triangle law of addition. The vector product of two quantities is declared to be the cross product.
Read More on Linquip
- Difference Between Energy and Power
- What is the Difference Between Oscillator and Crystal?
- Difference between Electric and Magnetic Fields
- Velocity Vs Acceleration: All You Should Know About
- Difference Between Current and Static Electricity
- Difference Between Hydraulics and Pneumatics
- Difference Between Period and Frequency
- Difference Between Mechanical and Electromagnetic Waves
What We Should Know About Vector Quantity
- Vector quantity implies that the physical quantity comprises of both magnitude and direction.
- Any change in vector quantity means changes either in magnitude or in direction or both.
- Vector quantities are one or two or three dimensional.
- Two vectors cannot be divided.
- Vector quantity follows the rules of any mathematical operation. The geometry method can be applied to solve the vector quantity.
- Mathematical calculation between two or more vector quantities can give either scalar or vector quantity.
- Mathematical operation between vector and scalar quantities often results in a vector quantity.
- A vector quantity can be resolved in two perpendicular directions by means of the adjacent angle.
Examples of Vector Quantity
Some examples of vector quantities are:
- Force
- Acceleration
- weight
- Shearing Stress
- velocity
- Electric field intensity
- Centrifugal force
- Torque
- Momentum
- Electric flux
Essential Difference Between Scalar and Vector Quantity
The following details are outstanding, so far as the difference between scalar and vector quantity is regarded:
- The scalar quantity is defined as the quantity that has only one characteristic, i.e., magnitude. The vector quantity is a physical quantity that has both magnitude and direction to be determined.
- Scalar quantities demonstrate one-dimensional quantities. In contrast, multi-dimensional quantities are described by vector quantity.
- A scalar quantity changes only when there is a change in its dimension. On the contrary, vector quantity varies with the change in its magnitude, direction, or both of them.
- scalar quantities follow ordinary rules of algebra to perform operations like addition, subtraction, and multiplication, while for the performance of functions, vector quantities follow vector algebra rules.
- When contrasting two scalar quantities, you have to respect only the magnitude. In contrast, both magnitude and direction are to be taken into account when comparing two vector quantities. In this way, vector quantities are a bit more complicated to deal with than scalar quantities.
- Finally, a scalar quantity can divide another scalar. However, this cannot be done in the case of a vector quantity.
Some Similarities Between Scalar And Vector Quantity
Scalar and vector quantity also have some similarities, which are presented here.
- Both scalar and vector quantity have some specific unit and dimension.
- Both scalar and vector quantity have magnitude.
- Both of these quantities are measurable.
- Both scalar and vector quantity can express specific physical quantities.
Scalar Product of Two Vectors
There are two ways for multiplying vectors; scalar product and vector product. The scalar of two vectors can be find by moving the part of one vector in the other direction and multiplying it in the other vector’s magnitude. The scalar product is also named the inner product, or dot product of vectors A and B are shown below.
A.B=\left| A \right| \left| B \right| \cos { (\theta ) }
in which
\left| A \right|= magnitude of vector A, \left| B \right|= magnitude of vector Band
\theta = angle between two vectors.If the parts of vectors are
A=({ A }_{ x },{ A }_{ y },{ A }_{ z })and
B=({ B }_{ x },{ B }_{ y },{ B }_{ z })the scalar product can be found by
A.B={ A }_{ x }{ B }_{ x }+{ A }_{ y }B_{ y }+{ A }_{ z }{ B }_{ z }
Conclusion
In summary, scalar quantity delivers you an idea about how much of an object there is. Still, vector quantity presents you with an indication of how much of an item there is and in which direction it is. Hence, the main difference between scalar and vector quantity is associated with the direction; in other words, scalars do not have direction, but vectors do. For more information, you can see here.



