Pump efficiency is equal to the power of the water produced by the pump divided by the pump’s shaft power input. A pump’s output power is determined by how much water and how much pressure it delivers. An electric motor or internal combustion engine delivers the shaft power to the pump.
The efficiency of a pump is defined by how well it can convert one kind of energy to another, as measured by the difference in horsepower flowing into and out of the pump. The horsepower entering the pump should ideally be equal to the horsepower exiting the pump, making the pumping system 100% efficient. There are various Pumps for Sale on Linquip from a range of Suppliers and Companies, as well as manufacturers and distributors.
Linquip’s website offers a comprehensive list of pump services to match your specific requirements. Vendors from Linquip can help you with this. To discover more about how to connect with a broad collection of Service Providers who consistently produce top-notch goods, please contact Pump Experts on Linquip.
It is important to choose an efficient pumping system that conserves fuel or electricity and lowers annual pumping costs. Poorly chosen and inefficient pumping systems can significantly increase annual costs. Also, there is a possibility of excessive wear occurring on the pumping plant, leading to water waste.
Also included in this article is a PDF file about pumps, their types, and their efficiency for further reading.
How We Write This Blog Post about Calculation of Pump Efficiency
To write a blog post about Calculation of Pump Efficiency, we would start by researching the topic and consulting with our experts in the field. We would then write an outline of the post and begin drafting it. During the drafting process, we would draw on our own experiences with Calculation of Pump Efficiency and use examples to illustrate key points. We would also consult with experts to ensure that our information is accurate and up to date. Once we have a draft of the post, we would revise it to ensure that it is clear, concise, and engaging.
What Is the Ideal Pump Efficiency?
Many medium and larger centrifugal pumps have efficiencies of 75 to 93 percent, and even the smallest ones have efficiencies of 50 to 70%. Large AC motors, on the other hand, may achieve a 97 percent efficiency, and any motor with ten horsepower or more can be built to surpass the 90% barrier.
The further your pump is from its optimal energy point, the more energy it will consume, making your system less dependable and efficient. This raises running expenses and raises the possibility of maintenance concerns.
Basics of Pump Efficiency
Efficiency describes how well a machine can convert one type of energy into another. Suppose a machine is provided a unit of energy, and its output is half that amount. In this case, its efficiency is 50%. As well, if a pump has 100 percent efficiency, the mechanical power input equals the water power output by the pump. There is no pump that is 100 percent efficient; therefore, the mechanical energy input will exceed the energy output. Frictional losses, leakages resulting from pressure differentials inside the pump case, and losses caused by more complex designs contribute to lower efficiencies.
Two simple but highly efficient machines are used a lot in the pump industry: centrifugal pumps and AC induction motors. Centrifugal pumps turn mechanical energy into hydraulic energy (flow, pressure, and velocity), and AC motors convert electrical energy into mechanical energy.
Most medium and larger centrifugal pumps have efficiencies in the range of 75 to 93 percent, while smaller pumps typically fall into the range of 50 to 70 percent. In contrast, large AC motors tend to have an efficiency close to 97 percent, and motors with ten horsepower or more can be designed to exceed 90 percent efficiency.
Based on the equation below, the overall pump efficiency can be determined by the ratio between the water power output and the shaft power input:
\eta =\frac{P_W}{P_S}\times 100\%
Where η is the pump efficiency. In addition, PW and PS represent water power and shaft power, respectively.
Pump efficiency can be calculated by considering two values, including pump flow rate and total head.
Flow Rate
Flow rate is an indicator of the amount of water flowing through a point at a specific time. With the help of a flow meter, you can measure the flow rate. While there are several types of flow meters, an ultrasonic flow meter is usually the easiest to use.
There is no restriction on the units this flow meter can measure, but gallons per minute is usually the unit used.

Total Head
In order to determine the total head, one has to measure the distance from the surface of the source water to the outlet of the pump, as well as the amount of pressure at the outlet of the pump. To calculate this value for a centrifugal pump, it is necessary to measure the distance from the water level to the pump outlet, as shown in the following diagram.
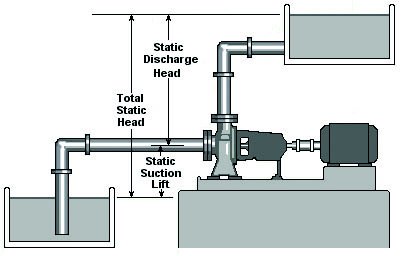
It is also necessary to measure the pressure at the pump outlet. This conversion is done knowing the fact that 2.306 feet of water equals 1 pound per square inch of pressure (psi), or in SI units, one meter seawater is equal to 10,000 Pa. For example, consider that the distance between the water surface and the pump outlet is 8 ft, and the pressure measured at the outlet is 60 psi. Therefore, it results in the total pressure head as follows:
H\ =\ 8\ +(60\times 2.306\ )=\ 146.4\ ft
And this value can be expressed in metrics, knowing that 1 psi is equal to 0.0689476 Pa:
H=146.4\times 0.0689476\cong 10.1\ Pa
Determining Pump Efficiency
As mentioned before, pump efficiency can be calculated by dividing the water (PW) power by the shaft power (PS).
Water Power Output
Pumps apply energy to develop the discharge pressure and deliver flow. Thus, the hydraulic horsepower of the pump is influenced by two factors multiplied by each other:
P_W=\ \left(p_2--p_1\right)\times Q
p1 and p2 are the pressure of the pump at the suction and discharge lines, measured in N/m2 (or psi), and Q is the flow delivered by the pump in m3/s (or gallons per minute).
Also, in the U.S. measurement system, PW can be expressed as:
P_W=\frac{HQ}{3960}
Using this system, H (the head of water) and Q (the flow rate) are both measured in feet and in gallons per minute.
With a constant 3960, the product of flow and head (in GPM-feet) can be converted to BHP.
Shaft Power Input
The pump power is supplied by an electric motor. The formula for calculating the output power of an electric driver is:
P_S\ =\ 1.732\times V\ \times I\ \times PF\ \times Motor\ Efficiency\times Coupling\ Efficiency
V is the measured motor voltage in Volts, I is the measured motor current in Amperes, and PF is the power factor. The motor efficiency can be obtained by calculating it through testing or considering it as the design efficiency. A supplier manual provides information about coupling efficiency.
In the U.S. customary units, PS is the power given to the pump shaft in brake horsepower (BHP).
For example, using these equations, we can predict that a pump that generates 90 GPM at 35 feet of head and needs 1 BHP has an overall efficiency at that flow point as:
\eta =\frac{P_W}{P_S}=\frac{\frac{90\times 35}{3960}\ }{1}\times 100\%=79.5\%
Heat balance across the pump can also be used to determine the actual power needed for the pump. The difference between the heat flow inlet and the heat flow outlet measures the pump power. This means that the fall in the efficiency of centrifugal pumps increases the liquid temperature at the pump discharge.
Different Categories of Pump Efficiency
Mechanical (ηm), volumetric (ηv), and hydraulic efficiency (ηh) each contribute to the overall efficiency of a pump. The bearing frame, stuffing box, and mechanical seals are the sources of mechanical losses. Volumetric efficiency is affected by leakage through wear rings, balancing holes, as well as clearances of the vanes in semi-open impellers. Fluid friction and volute and impeller losses are considered as part of hydraulic efficiency.
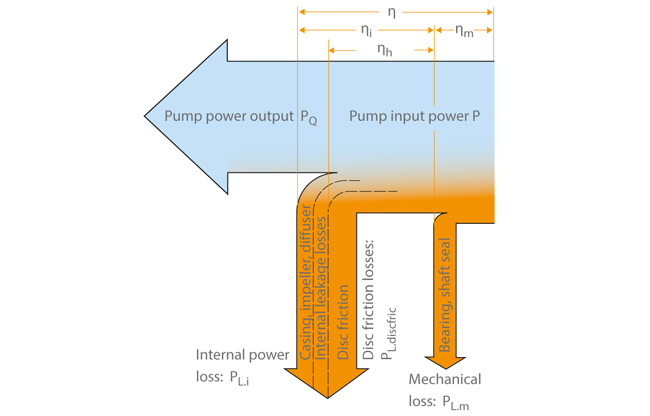
However, despite mechanical and volumetric losses being important, hydraulic efficiency is more influential.
Volumetric Efficiency
The volumetric efficiency of a pump is determined by the ratio of the actual flow delivered by it to its theoretical flow at a given pressure. Pump displacement per revolution and driven speed are multiplied to determine the theoretical flow. For example, if the pump has a displacement of 200 cc/rev and is turning at 500 RPM, the flow rate is 100L/min.
{\eta }_v=\frac{Actual\ flow\ rate\ by\ the\ pump}{Theoretical\ flow\ rate}\times 100\%
or
{\eta }_v=\frac{Q_A}{Q_T}\times 100\%
Flow meters must be used to measure the actual flow. In the above example, if the pump actually flowed 90 liters per minute in the testing, we can say the pump is 90% efficient.
Volumetric efficiency is the most common metric used to determine hydraulic pump condition – based on an increase in internal leakage caused by wear or damage. If the flow meter did not take into account theoretical flow, the actual flow would be meaningless.
During the design of a system, engineering designers calculate the flow capacity of a pump at a particular pressure based on its volumetric efficiency value. It is important to realize that leakage paths within a pump usually remain constant when calculating volumetric efficiency based on flow tests. As a consequence, if a pump is tested at less than its full displacement (or maximum RPM), this will incorrectly calculate efficiency – unless leakage is treated as a constant and adjusted accordingly.
Consider the case of a variable displacement pump whose maximum flow rate is 100 liters/minute. In the case of flow rate measurement of 90 liters/minute, the calculated volumetric efficiency is 90%. For a pump that is flow tested at half displacement (50 L/min) at the same pressure and flow temperature, leakage losses will still remain 10 L/min, and so the calculated volumetric efficiency is 80%.
The second calculation is not incorrect, but it does need clarification: this pump is 80 percent efficient at half its displacement. Due to the relatively constant leakage losses of 10 L/min, a pump tested under the same conditions will be 90% efficient at 100% displacement (100 L/min) – but 0% efficient at 10% displacement (10 L/min).
If you visualize the various leakage paths as fixed orifices, then you can explain why pump leakage is constant at any given pressure and temperature. The fluid flow rate through an orifice is a function of its diameter (and shape), fluid pressure drop, and viscosity. Accordingly, if these variables do not change, leakage will remain constant, regardless of displacement or shaft speed.
Mechanical/Hydraulic Efficiency
To determine the mechanical/hydraulic efficiency of a pump, the actual drive torque required and its theoretical torque are compared. Mechanical/hydraulic efficiency of 100% means the hydraulic pump needs no torque to provide flow at zero pressure. In reality, mechanical and fluid frictions prevent this from happening.
{\eta }_m=\frac{Pump\ output\ power\ assuming\ no\ leakage}{Actual\ power\ delivered\ to\ pump}\times 100\%
or
{\eta }_m=\frac{p\times Q_T}{T_A\times N}\times 100\%
p is the discharge pressure of the pump, QT is the theoretical pump flow rate, TA is the actual torque delivered to the pump, and N is the rotational speed of the pump shaft.
The mechanical efficiency of a pump can also be calculated by considering torque:
{\eta }_m=\frac{Teoretical\ torque\ required\ to\ drive\ the\ pump}{Actual\ torque\ provided\ to\ the\ pump}\times 100\%
or
{\eta }_m=\frac{T_T}{T_A}\times 100\%
This is sometimes called torque efficiency, which is a function of speed and fluid viscosity. As viscous friction is viscous-dependent, higher pump speeds result in lower efficiency. Despite reducing viscous losses, lower viscosity negatively impacts volumetric efficiency.
There are many similarities between the design phases of the centrifugal pump and the induction motor. They have similar features in that each can be modified by the designer by changing only two major components. A motor consists of a rotor and a stator. Centrifugal pumps, however, use their impeller and volute (or diffuser) to move fluid. The impeller is the first component to investigate when assessing centrifugal pump efficiency.
For any impeller, we know that its head varies as a square of the change in speed. By doubling the speed, the head will increase four times as much. The same applies to small changes in diameter if you keep the speed constant. Similar principles apply to flow through an impeller, but here it is directly proportional to the change in diameter or speed—double either, and the flow will double. The change in rotational speed or diameter of an impeller actually refers to the peripheral speed of a point at its periphery. This speed determines how much head and flow an impeller can produce.
For any impeller, we know that its head varies as a square of the change in speed. By doubling the speed, the head will increase four times as much. The same applies to small changes in diameter if you keep the speed constant. The performance of an impeller is also affected by factors such as vane shape.
Today, the starting point of the design of a pump is “specific speed.” It is expressed based on the rotational speed, head, and flow rate, as follows:
N_S=\frac{nQ^{\frac{1}{2}}}{H^{\frac{3}{4}}}
In conclusion, overall efficiency is determined by multiplying efficiencies together. Based on an input flow and pressure, the overall efficiency can be used to determine how much drive power is needed for a hydraulic pump. The more efficient the pump, the less energy it will use for a given flow rate and pressure, and the less efficient, the more energy will be lost to heat.
\eta ={\eta }_v{\eta }_m
\eta =\frac{pQ_A}{T_AN}\times 100\%
To learn more about pumps, you can read the following PDF.
Factors Affecting Pump Efficiency
The efficiency of a centrifugal pump is influenced by various factors:
- The minimum thermal flow is maintained in recirculation lines to prevent cavitation during low flow pump operation. As an inevitable result, the pump becomes less efficient.
- The internal surface roughness is an important consideration. Smooth surfaces in pump internals contribute to high efficiency.
- The efficiency of centrifugal pumps decreases as wear rings clearance increases. The wear rings reduce the clearance between the pump casing and the impeller.
- A higher fluid viscosity reduces pump efficiency.
- The efficiency will decrease due to mechanical losses in couplings, bearings, packings, and so on.
- The trimming of impellers will decrease efficiency.
Download Pump Efficiency PDF
Buy Equipment or Ask for a Service
By using Linquip RFQ Service, you can expect to receive quotations from various suppliers across multiple industries and regions.
Click Here to Request a Quotation From Suppliers and Service Providers
Read More In Linquip
- Heat Pump Efficiency: Types and Equations
- Different Types of Pumps: Ultimate Guide in 2021
- Efficiency of Inverter
- Electric Heater Efficiency and Running Costs
- Efficiency of Fuel Cell: Calculation Formula & Equation
- Space Heater Efficiency For Various Types of Heater
- Heater Efficiency Calculation: Formula & Equation
- Fan Efficiency Calculation: Formula & Equation
- Efficiency of Wind Turbines
- DC Motor Efficiency: Calculation: Formula & Equation
- Efficiency of Diesel Generators Calculation: Formula & Equation
- Energy Efficient Electric Heater: A Practical Guide
- What is Generator Efficiency? Calculation & Formula Guide
- Efficiency of Induction Motor: Calculation & Equation
- Optimize Your Pump System with Linquip’s Pump Flow Rate Calculator



