Efficiency of Wind Turbines

In 1919, German physicist Albert Betz hypothesized the Betz limit as the maximum efficiency of wind turbines. In his study, Betz determined this value as 59.3%, meaning that not more than 59.3% of the kinetic energy in the wind can be used to spin a turbine and produce electricity. A turbine cannot reach the Betz limit, and typical efficiency levels range from 35% to about 50%.

A wind turbine extracts energy by reducing the speed of passing winds. In order for a wind turbine to be 100% efficient, all wind would have to stop completely after it contacts the turbine. As long as the air does not move all the way to the back of the turbine, it will prevent other air from coming in, which will stop the turbine from spinning.

This article includes a PDF for readers interested in learning more about the efficiency of wind turbines.

Basics of Wind Turbines

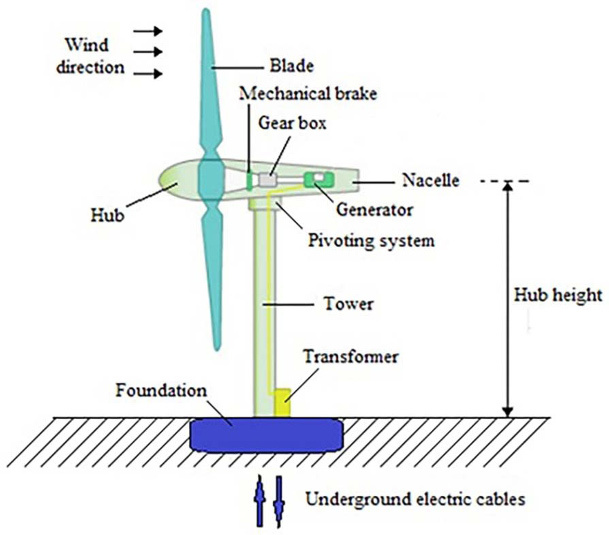
A wind turbine operates by converting the kinetic energy in the wind into mechanical energy, which is used to spin a generator to generate electricity. Wind turbines can either be installed onshore or offshore. Despite the broad range of sizes available today, all types of wind turbines are generally made up of several main components, including rotor blades, nacelle, and tower.

Rotor 

In wind turbines, the blades work the same way as the wings of an aircraft. The blades are curved on one side and flat on the other. In a blade with a curved edge, the wind flows more quickly, causing pressure differences on either side. To equalize the pressure difference, the air pushes the blades, causing the blades to rotate.

Nacelle 

Generators and gears make up the nacelle. Utilizing the gears, the rotating blades are connected to the generator. With gears, the blade rotation is converted into the generator rotation speed of about 1500 rpm. Afterward, the rotational energy from the blades is converted into electrical energy by the generator.

Tower 

On top of the tower are the blades and nacelle. A tower holds the rotor blades above the ground at a wind speed ideal for the operation. The height of towers is typically between 50 and 100 meters above ground or water. Towers offshore are typically fixed to the water bottom, though research is being conducted to develop a tower that can float.

Betz’s Law 

Betz’s law determines how much power is possible to extract from the wind, independent of how a wind turbine is designed. On the basis of the principles of conservation of mass and momentum, this law determines that when an airstream passes through an idealized “actuator disk,” it captures energy from the wind stream. Betz’s law states that no turbine is capable of capturing more than 16/27 (59.3%) of the wind’s kinetic energy. The value of 16/27 (59.3%) is known as Betz limit or Betz’s coefficient. Wind turbines at utility-scale are typically capable of producing 75–80% of the Betz limit at peak.

Calculations for an open-disk actuator yield the Betz limit. By using a diffuser to collect more wind flow and directing it through the turbine, the energy can be extracted more, but the Betz limit still is used for the cross-section of the whole structure.

This limit defines the maximum amount of energy that can be extracted at a given location every year. There would be no possibility of obtaining more energy than the Betz limit from the wind, even if it blows continuously for a year.

Increasing economic efficiency is essentially a function of increasing production per unit, measured by square meters of the blade. To reduce the cost of electrical power production, system efficiency needs to be improved. It may be possible to increase efficiency and power generation from wind capture devices by engineering them, for instance, by changing the arrangement and dynamics of wind turbines. Efficiency improvements in power transmission, storage, or application may lower power per unit costs.

The Assumptions for Calculating the Betz Limit 

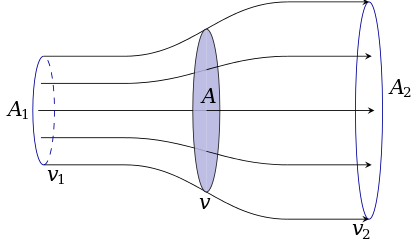
A disc can be substituted for the wind turbine in order to calculate its maximum theoretical efficiency. Such a disc would withdraw energy from the fluid flowing through it. After passing through this disc, the fluid flows with a reduced velocity at a certain distance behind it.

A disc of this kind possesses the following characteristics:

• The rotor possesses an infinite number of blades without a hub and has no drag. This idealized value would be lowered by any resulting drag.
• The air flows axially into and out of the rotor. Using a control volume analysis, all flow entering and leaving the control volume must be accounted for, and failing to do so would breach the conservation equations.
• The air flow is considered incompressible, and the density remains constant.
• No heat transfer occurs.
• The rotor or disc receives a uniform thrust.

Using these hypotheses, as mentioned above, the power output of a wind turbine is obtained by utilizing the laws of mass and momentum conservation to the air control volume as follows:

 

P=\frac{1}{2}\rho Av\left(v^2_1-v^2_2\right)

 

and,

 

v=\frac{1}{2}\left(v_1+v_2\right)

 

This means v is the wind velocity at the rotor as the average of the air velocities at upstream (v₁) and downstream (v₂). Also, A is the rotor swept area, and ρ is the air density.

Using mathematical operations, maximum wind turbine output power can be obtained as follows:

 

P_{max}=\frac{16}{27}\times \frac{1}{2}\rho Av^3_1

 

Therefore, the power that can be obtained from a cylinder of fluid with a cross-sectional area of A and velocity of v₁ is expressed as:

 

P=\frac{1}{2}C_{p}\rho Av^3_1

 

In this equation, C_p is the power coefficient and can be calculated by:

 

C_p=\frac{P}{P_{wind}}

 

In which, P_wind is the power in a moving fluid in a cylinder with a cross-sectional area of A and velocity of v₁:

 

P_{wind}=\frac{1}{2}\rho Av^3_1

 

The power coefficient has a maximum value of:

 

C_{p,max}=\frac{16}{27}=0.593

 

Here is a PDF that explains in detail how the Betz limit is calculated and how Continuity and Mass Conservation Laws are applied in this particular case.

Maximum Efficiency of a Wind Turbine

Today’s wind turbines can reach maximum values of Cp in the range of 0.45 to 0.50, which is 75–85% of the maximum theoretical value. If wind speeds are high and a turbine is running at its rated power, the turbine rotates (pitches) its blades to reduce Cp to avoid damage. From 12.5 to 25 m/s, the wind power increases by a factor of 8, so Cp must fall accordingly, decreasing to 0.06 for winds of 25 m/s.

There is no dependence of the Betz limit on the geometry of the wind extraction system, provided that the flow passes through the control volume and exits the control volume with uniform velocity. Since this analysis was idealized to disregard friction, any extraneous effects will only reduce the performance of the turbine. A non-ideal effect would detract the fluid energy, thereby lowering its overall efficiency.

Contradictions

A balance of energy across the rotor plane was used in 1934 by H. Glauert to derive the equation for turbine efficiency, which considers the angular component of velocity. The Glauert model predicts an efficiency that is below the Betz limit and nears this value as the tip speed ratio approaches infinity.

A solvable model (GGS), introduced by Gorban, Gorlov, and Silantyev in 2001, addresses non-uniform pressure distributions and curvilinear flow over the turbine plane (issues that were not considered in Betz’s method). According to the GGS model, peak efficiency is reached at approximately 61% of the total flow through the turbine, which is also similar to the Betz result of 2/3 for a flow leading to the maximum efficiency, but GGS predicts a much smaller peak efficiency: 30.1%.

In recent years, computational fluid dynamics (CFD) has been used to model wind turbines and is showing good agreement with experimental results. The optimal efficiency computed with CFD typically lies between the Betz limit and the GGS solution.