Velocity vs acceleration both express motions, but there is an essential distinction between these two concepts. Understanding the differences between velocity vs acceleration is necessary if you’re studying physics at a high school or college level. Knowing what velocity suggests leads to an understanding of what acceleration indicates because while velocity is the rate of position change, acceleration is the rate of velocity change. If you are traveling at a constant speed, you have velocity but no acceleration, but if you are moving and your pace is shifting, you have velocity and acceleration. In this article, we are going to examine the difference between velocity vs acceleration clearly. But before that, some essential explanations about each of them is necessary.
What Is Velocity?
The rate of your position shift with time determines your velocity. In everyday language, velocity indicates the same thing as speed. Nevertheless, in physics, there is an essential distinction between the two titles. Speed is a “scalar” quantity, and it is estimated in units of distance/time, so in miles per hour or meters per second. Velocity is a “vector”, so it has both a magnitude and a direction. Technically, assuming you are progressing at ten meters per second is a speed; saying you are traveling at 10 meters per second towards the north is a velocity since the latter has a direction.
The formula for velocity is as follows:
v=\frac { \Delta x }{ \Delta t }
In which v represents velocity and Δx, and Δt are distance traveled and time is taken, respectively. In calculus’s language, it can be more accurately defined as the rate of change of position concerning time. So, it is provided by the derivative of the equation for the position with respect to time.
What Is Acceleration?
Acceleration is the rate of velocity change with time. Similar to velocity, this is a vector quantity that possesses a direction as well as a magnitude. A velocity increment is regularly called acceleration, while a drop in velocity is sometimes termed deceleration. Technically, because velocity comprises a direction as well as a speed, a shift in direction at a constant speed is still supposed acceleration. Acceleration can be represented simply as:
a=\frac { \Delta v }{ \Delta t }
Acceleration, a, has units of distance/time squared, for instance, m/s2.
In calculus’s language, this is more specifically described as the rate of velocity change with respect to time, so it is determined by taking the derivative of the velocity expression with respect to time. Alternatively, you can attain it by taking the second derivative of the expression for the position with respect to time.
Velocity vs Acceleration?
To describe velocity vs acceleration, let us first describe each term separately. Moving with a constant velocity suggests you are continuously going at the same speed in the same direction. If you have a constant velocity, this indicates you have zero acceleration. You can visualize this as driving down a straight road but holding your speedometer on the same value.
Constant acceleration is pretty different. If you move with a constant acceleration, your velocity will always vary, but it changes by a consistent amount each second. The acceleration due to gravity on the Earth has a constant value of 9.8 m/s2, so you can perceive this like dropping something from a tower. The velocity begins low but rises by 9.8 m/s for every second it is falling under gravity.
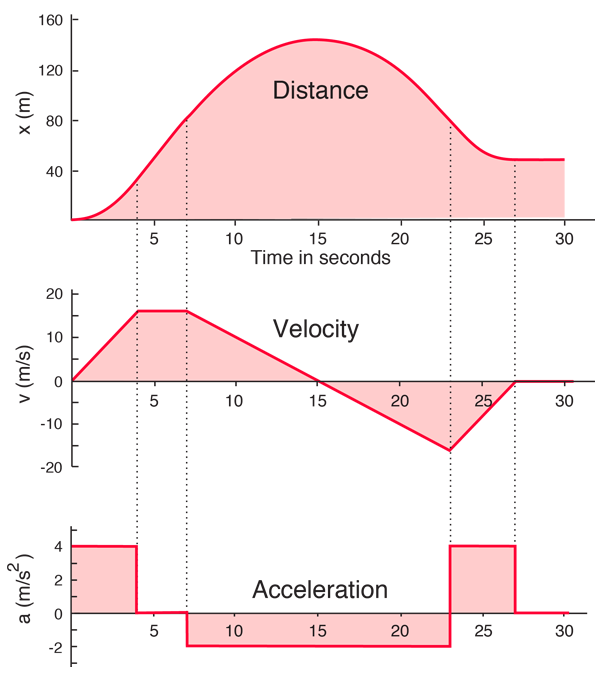
The above-mentioned descriptions clearly show what is the difference between Velocity vs acceleration.
Velocity and Momentum
The equation for momentum applies velocity rather than acceleration. Momentum is p = mv, where p is momentum, m is mass, and v is velocity. In the second law of Newton, acceleration multiplied by mass transmits force, whereas when velocity is multiplied by mass, this provides the momentum. Their definitions are diverse, and this reveals how those distinctions lead to differential equations in practice.
Acceleration and Newton’s Second Law
Acceleration, rather than velocity, produces a crucial part of the second law of Newton. The equation is F = ma, where F is force, m is mass, and a is the acceleration. Due to the link between velocity and acceleration, you can also write this as force = mass × the velocity rate. Nevertheless, acceleration is the key component here, not velocity.
Acceleration Calculation
Kinematics is the part of physics that explains the basics of motion, and you are often tasked with obtaining one quantity given knowledge of a couple of others. Learning the constant acceleration equations sets you up well for this type of problem. If you have to attain acceleration but only have a starting and final velocity, you can determine the acceleration along with the distance covered. You only require the right one of the four equations and a little bit of algebra to obtain the expression you need.
Equation of Constant Acceleration
There are four principal constant acceleration equations that you’ll require to determine all problems like this. They are only legitimate when the acceleration is “constant,” so when something is accelerating at a steady rate rather than accelerating faster and faster as time goes on. Acceleration due to gravity can be utilized as an example of constant acceleration, but problems often define when the acceleration continues at a constant rate.
The constant acceleration equations utilize the following symbols: a is acceleration, v denotes final velocity, u indicates starting velocity, s expresses displacement, and t is time. The equations state:
v=u+at
s=0.5(u+v)t
s=ut+0.5a{ t }^{ 2 }
{ v }^{ 2 }={ u }^{ 2 }+2as
Various equations are beneficial for different situations, but if you only have the velocities v and u, along with distance s, the last equation absolutely satisfies your needs.
Rearrange the Equations for Acceleration
Get the equation in the right form by rearranging. You can rearrange equations though you like, provided you do the identical thing to both sides of the equation in each step.
Beginning from:
{ v }^{ 2 }={ u }^{ 2 }+2as
Subtract u2 from both sides to get:
{ v }^{ 2 }-{ u }^{ 2 }=2as
Divide both sides by 2s and modify the equation to get:
a=\frac { { v }^{ 2 }-{ u }^{ 2 } }{ 2s }
This indicates how to obtain acceleration with velocity and distance. Remember, though, that this solely applies to constant acceleration in one direction. Things become a little more complex if you have to attach a second or third dimension to the motion. Still, basically, you create one of these equations for movement in each direction individually. There is no easy equation like this to use for a varying acceleration, and you have to apply calculus to solve the problem.
An Example of Constant Acceleration Calculation
Assume a car progressıng with constant acceleration, with a velocity of 36 (km/h) (10 m/s) at the beginning of a 1 kilometer (1,000 meters) long track, and a velocity of 180 (km/h) (50 m/s) by the end of the road. We want to determine the constant acceleration. Apply the equation from the last section, considering v is the ultimate velocity and u is the starting velocity. So, you have v = 50 m/s, u = 10 m / s and s = 1000 m. Embed these into the equation to get:
a=\frac { { 50 }^{ 2 }-{ 10 }^{ 2 } }{ 2\times 1000 } =\frac { 2400 }{ 2000 } =1.2\quad m/{ s }^{ 2 }
So, the car accelerates at 1.2 meters per second squared throughout its travel across the road, or in other words, it gets 1.2 meters per second of speed every second.



