When describing objects’ motion in terms of distance, time, and direction, physicists use the fundamental quantities of speed vs velocity. Two words, two separate meanings. Yet, not unusually, we hear these terms employed interchangeably. So, what’s the exception? Why is it inaccurate to utilize the terms speed vs velocity interchangeably?
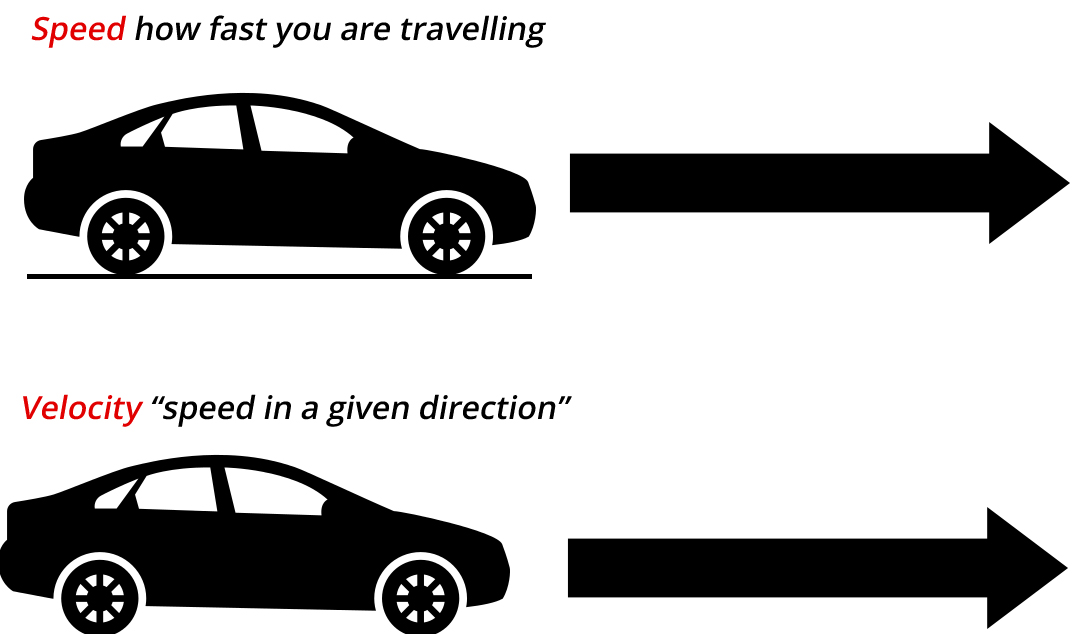
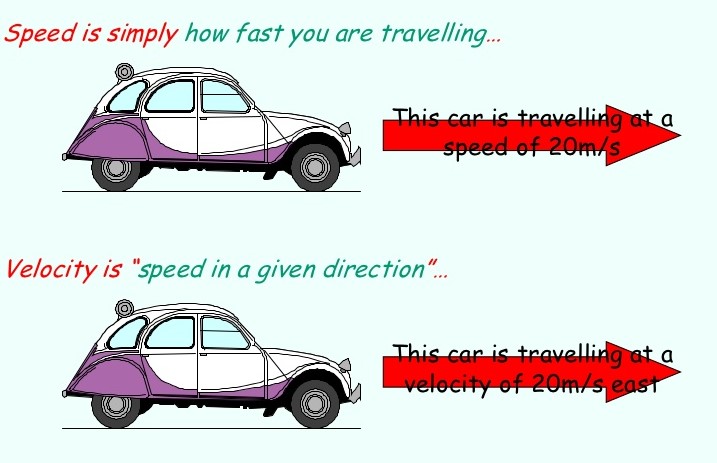
The same as distance and displacement, which have different meanings (despite their similarities) indeed, speed vs velocity has some differences. Speed is a scalar quantity that relates to “how fast an object is traveling.” Speed can be considered as the rate at which an object crosses distance. A fast-moving object has a great speed and covers a comparatively large distance in a short time. In contrast, a slow-moving thing with a low speed covers a comparably small distance in the same amount of time. An object with no progress at all has zero speed. For example, 80 km/hr represents the speed at which a car travels along a road, while 80 km/hr east illustrates the velocity at which it travels.
Velocity as a Vector Quantity
Velocity is a vector quantity that relates to “the rate at which an object alters its position.” Visualize a person rushing, i.e., one step ahead and one step back, forever returning to the origin position. While this might occur an excitement of activity, it would follow with a zero velocity. Because the person permanently reverts to the original position, the movement would never change the situation.
Since velocity is determined as the rate at which the position switches, this motion results in zero velocity. If a person in motion hopes to maximize their velocity, they must make every attempt to maximize the amount they are relocated from their original position. Every step must go into driving that person further from where he or she began. For sure, the person should never change directions and start to return to the original position.
As mentioned before, velocity is a vector quantity; thus, it is direction aware. When evaluating the velocity of an object, one must maintain track of direction. It would not be sufficient to say that an item has a velocity of 80 km/hr. One must incorporate direction information to describe the velocity of the object entirely. For example, you must define an object’s velocity as being 80 km/hr, west. This is one of the basic differences between speed vs velocity. Speed is a scalar quantity, which implies it does not keep track of direction; velocity is a vector quantity and direction-aware.
Direction of the Velocity Vector
The task of representing the direction of the velocity vector is straightforward. The direction of the velocity vector is solely the same as the direction that an object is traveling. It would not matter whether the item is advancing up or postponing. If an object is shifting rightwards, then its velocity is defined as being rightwards.
If an object is traveling downwards, then its velocity is represented as being downwards. So an airplane moving towards the east with an 800 km/hr speed has a velocity of 800 km/hr, east. Note that speed has no direction; as mentioned before, it is a scalar, and the velocity at any moment is solely the speed value with a direction.
What’s the Difference Between Speed and Velocity?
Speed vs velocity both measure the motion rate of an object. Nevertheless, speed is a scalar quantity, which suggests that it can be expressed with a numerical value. However, velocity is a vector quantity, which depends on the direction as well as magnitude.
- speed – the rate of distance covered by a moving object over time
- velocity – the rate of displacement of a traveling object over time
Fundamentally, an object’s speed indicates how fast it is moving. Its velocity, however, shows you how fast it is moving in a specific direction. You apply speed measurements in your daily life, but physicists depend on velocity measurements more regularly in their work.
Average Speed versus Instantaneous Speed
Since a moving object frequently alters its speed during its motion, it is frequent to distinguish between the average speed and the instantaneous speed. The difference is as follows.
- Instantaneous Speed – the speed at any provided instant in time.
- Average Speed – the average of all instantaneous speeds; determined merely by a distance/time ratio.
You might consider the instantaneous speed as the speed that the speedometer records at any provided instant in time and the medium speed as the average of all the speedometer readings through the progression of the journey. Since the assignment of averaging speedometer readings would be pretty complicated, the average speed is more ordinarily calculated as the distance/time ratio.
Moving objects do not regularly travel at random and changing speeds. Irregularly, an object will travel at a constant speed and a steady rate. That is, the item will satisfy the same distance every fixed interval of time. For example, a cross-country runner might be moving with a constant speed of 10 m/s in a straight line for several minutes. If his/her speed is consistent, then the distance covered every second is the same. The runner would travel a distance of 10 meters every second.
If we could measure his/her location (distance from an optional starting point) each second, we would perceive that the position would change by 10 meters each second. This would be in severe contrast to an object that is adjusting its speed. An object with a dynamic speed would be moving a distinct distance each second.
Equations for Speed and Velocity
As an object progresses, it often experiences speed changes. For instance, during an average school trip, there are many speed changes. Rather than the speed-o-meter keeping a steady reading, the needle continually moves up and down to indicate the stopping and starting and the accelerating and decelerating. One moment, the car may be moving at 80 km/hr, and another moment, it might be terminated (i.e., 0 km/hr).
Still, during the school trip, the person might have an average speed of 32 km/hr. The average speed during a complete motion can be thought of as the average of all speedometer readings. If the speedometer readings could be obtained at 1-second intervals and then averaged together, the average speed could be resolved.
It is most straightforward to see the distinction between speed and velocity when you examine their equations. In order to measure the speed of an object(s), you should measure its distance (d) over time (t):
s=d/t
Once you identify the object’s speed, you can determine its velocity by calculating the displacement (d) over time (t):
v=d/t
For instance, let us say that a car covers 100 kilometers in one hour. When you put in the equation, you get:
s=100/1=100 km/hr
So the car is traveling 100 kilometers per hour. But that equation does not inform you that much of that trip was in a circle, westward bound, and the car parks only 50 kilometers from where it began. So the velocity would be:
v=50/1=50 km/hr west
This knowledge may not seem straightforward for an everyday commuter, but it is imperative to know the distinction between the speed of an object and its velocity when studying physics. When they are the same value, the object has progressed in a straight line. Inconsistent values between speed and velocity designate that the object’s path was not straight.
Conclusion
Knowing how fast you are progressing or are capable of going, helps drivers, runners, cyclists, and anyone who can understand a speedometer. But speed is merely the starting point for many valuable concepts in physics. Check out additional resources on velocity, an excellent video comparing speed vs velocity.



