Transformers form the most crucial connection between supply systems and load. The transformer efficiency directly influences its performance and aging. The transformer efficiency, in general, is in the range of 95 – 99 %. For large power transformers with shallow losses, the efficiency can be as high as 99.7%.
The transformer’s input and output measurements are not performed under loaded situations as the wattmeter readings necessarily have 1 to 2 percent errors. Thus, for the purpose of efficiency estimations, OC and SC examinations are employed to calculate rated core and winding losses in the transformer.
The core losses depend on the rated voltage of the transformer, and the copper losses depend on the currents within the transformer primary and secondary windings. Therefore, transformer efficiency is of special importance to operating it under constant frequency and voltage conditions. The rise in the transformer’s temperature due to heat produced influences the life of transformer oil properties and determines the type of cooling method chosen. The temperature rise restricts the rating of the equipment.
How to Determine Transformer Efficiency?
Before talking about important facts about transformers, we must first explain the transformer efficiency. Fundamentally, any transformer on earth has input and output powers. We understand that the output power is virtually smaller than the input power due to the power losses of transformers.
Hence, the efficiency can be defined as the ratio between the output power and the input power as is obvious from the subsequent equations:
we can render efficiency as
\eta=(\frac{Output~power}{Input~power})\times100
which implies
\eta=(\frac{Output~power}{Output~power+Losses})\times100
The losses generally comprise copper losses in the windings + the iron loss + dielectric loss + stray load loss,
\eta=(\frac{Output~power}{Output~power+Iron~loss+Copper~loss+Dielectric~loss+Stray~load~loss})\times100
Also, it can be represented as
\eta=(\frac{Input~power- Iron~loss-Copper~loss-Dielectric~loss-Stray~load~loss}{Input~power})\times100
\eta=1-(\frac{Iron~loss+Copper~loss+Dielectric~loss+Stray~load~loss}{Input~power})\times100
So, the transformer efficiency can be obtained from any equation mentioned above according to the provided data.
Here, we are going to describe each mentioned loss for the calculation of transformer efficiency.
Power Losses
The iron losses comprise the hysteresis and eddy current losses in the transformer. These losses depend on the flux density inside the core, which mathematically described as,
Hysteresis Loss:
P_h=k_hfB_{max}^n
Eddy Current Loss:
P_e=k_ef^2B_{max}^nt^2
Where kh and ke are constants, Bmax is the top magnetic field density, f is the frequency of the source, and t denotes the thickness of the core. The power ‘n’ in the hysteresis loss is recognized as the Steinmetz constant, whose value can be nearly 2.
Thus,
Total~iron~or~core~losses(P_i)=Hysteresis~loss+Eddy~current~loss
The dielectric losses happen inside the transformer oil. For low voltage transformers, it can be ignored.
The leakage flux ties to the metal frame, tank, etc., to generate eddy currents and are present all around the transformer, therefore, designated as stray loss, and it depends on the load current and so identified as ‘stray load loss.’ It can be described by resistance in series to the leakage reactance.
EMF Equation of Transformer– Turns Voltage Transformation Ratio of Transformer
Essential Facts
Here, we want to mention some valuable facts about transformer efficiency.
The First One
Is there any transformer that possesses an efficiency of 100 %?
The ideal transformer has an efficiency of 100%. In these transformers, the input power is equivalent to the output power. Nevertheless, this transformer is not feasible in reality. It is only a case for scientific and theoretical studies.
The Second One
Why do we examine and study the transformer efficiency?
In fact, there are thousands but millions of scholars worldwide chanting the transformer efficiency equations every day, but without real knowledge of the purpose of studying and investigating it.
As a matter of fact, we analyze and interpret transformer efficiency to discover the performance of the transformer, which is, of course, revealed on the economic side.
And all of us know that the higher the transformer efficiency, the less power lost in the transformer, the costs of periodical transformer’s maintenance, and the transformer’s energy consumption cost.
The Third One
Does loading the transformer have any influence on the transformer efficiency?
It suggests that the efficiency may be variable depending on the load of the transformer.
Many essays express calculating the transformer efficiency but do not specify that the transformer is more than efficient and where the disagreement happens.
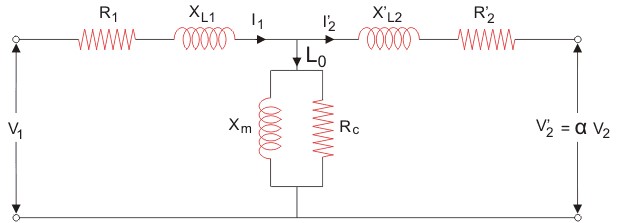
What is the Equivalent Circuit of Transformer?
And Here Comes the Necessary Question: Is the Efficiency of The Transformer Fixed or Variable?
Let us interpret it with the equations as it is the best proof to answer this question.
By studying the transformer losses, we find two kinds of losses: copper loss and iron loss.
Assume a transformer has a power of 1000 kVA, and the iron losses are 1.2 kVA. In the case of the no-load condition, the value of the copper losses is zero.
By putting the variables in the mentioned equations, we have
\eta=(\frac{input~power-iron~loss-copper~loss}{input~power})\times100
\eta=(\frac{1000-1.2-0}{1000})\times100=99.88\%
In the situation of the load condition, copper losses possess a value, suppose that is 10 KVA.
Therefore,
\eta=(\frac{1000-1.2-10}{1000})\times100=98.88\%
Accordingly, the higher the load, the higher the copper losses, and the lower the efficiency.
Considering this fact, we can conclude the maximum efficiency that the transformer can reach.
So, We Can Determine the Equation of Maximum Efficiency of Transformer:
Assume that (X) is the fraction of the full load, then compensation in the equation of efficiency results in:
X\eta=(\frac{Xoutput~power}{Xoutput~power+Xiron~loss+Xcopper~loss})\times100
The copper losses alter according to the loading of the transformer condition.
Furthermore, efficiency will be highest if the denominator concerning the changeable copper losses is equated to zero.
We can presume that we will obtain maximum efficiency if copper losses (Pc) are equivalent to iron losses (Pi).
So,
\eta_{max}=(\frac{output~power}{output~power+P_i+P_c})\times100\%
P_c=P_i
At maximum efficiency condition,
\eta_{max}=\frac{output~power}{output~power+2P_i}\times100\%
Besides, copper losses are:
P_C=x2P_C
where Pc is the full load coper losses.
In the condition of maximum efficiency, we have:
P_i=X2\times P_c
X=\sqrt{\frac{P_i}{P_c}}
Therefore,
\eta_{max}=X\times full~load~KVA
\eta_{max}=\sqrt{\frac{P_i}{P_c}}\times full~load~KVA
The Fourth One
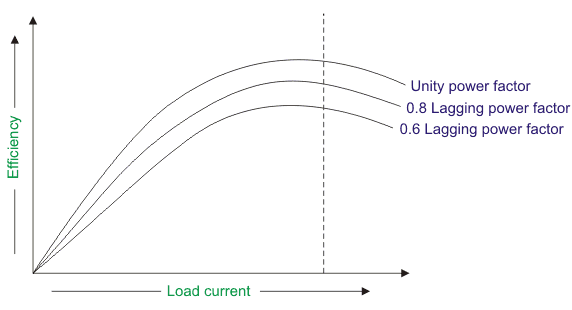
Does the power factor of the load impact the efficiency of the transformer?
Repeatedly, we will explain in numbers as is the best proof to confirm the facts:
- Assume there is a transformer with a power of 100 kVA and the iron losses are 0.2 kVA, and in the secondary coil, the current is 8 amperes with a lag power factor of 0.8, next:
Coper~losses=V2\times I2\times Cos \Phi=220\times 8\times 0.8=1.41~KVA
\eta=(\frac{input~power-iron~loss-copper~loss}{input~power})\times 100\%
\eta=\frac{100-0.2-1.41}{100}\times100\%=98.39\%
For the identical transformer and the identical load but in the secondary coil, the current is 8 amperes with a 0.6 lag power factor, we have:
(P_c)~Coper~losses=V2\times I2\times Cos \Phi=220\times 8\times 0.6=1.06~KVA
\eta=(\frac{input~power-iron~loss-copper~loss}{input~power})\times 100\%
\eta=\frac{100-0.2-1.06}{100}\times100\%=98.47\%
Hence, the greater the load power factor, the smaller the efficiency when the load is constant.
The Fifth One
Is the efficiency of the transformer assessed and examined only instantly?
After distinguishing the above facts, we can recognize that the transformer efficiency is changeable all the time, but will the efficiency be examined and recorded every minute, hour, day, or month?
As we described earlier, this efficiency has various factors. Most essential, the download and the loading are not solidified; we have to manage a comprehensive study every hour to create a daily report to analyze the transformer efficiency.
But how is the transformer efficiency measured throughout the day? The answer is sincere and lies in the following equations:
\eta=(\frac{input~power-iron~loss-copper~loss}{input~power})\times 100\%
Note that iron loss is solidified all day, and Copper loss varies according to the loading condition
\eta~(for~24~hour)=\frac{(input~power-iron~loss)-(\Sigma~copper~loss~for~24~hours/24)}{input~power}\times 100\%
Conclusion
We have comprehensively discussed the transformer efficiency and the way of its calculation. We have also stated the importance of it and the procedure of determining it on a daily basis. Nevertheless, for a better understanding of transformer efficiency, watch this fantastic video.



