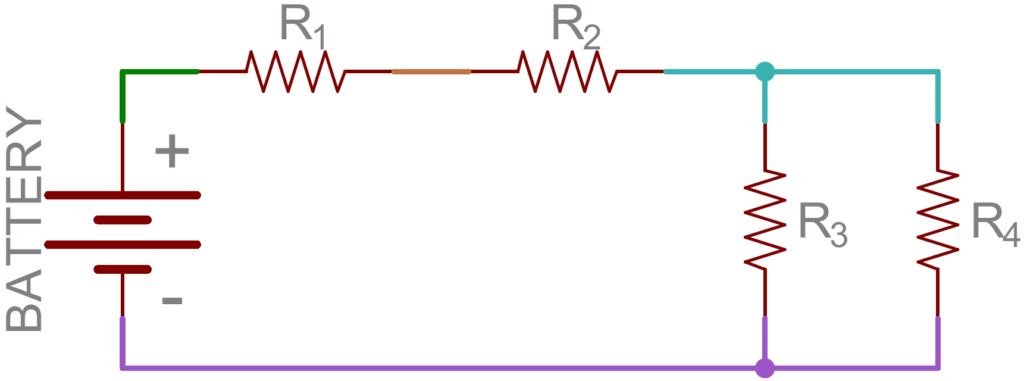
Series and Parallel Circuit_ Close circuits have a complete path for current to flow in a loop. An open circuit does not have a closed-loop, which means that it’s not operative. A short circuit is a low-resistance path, usually made accidentally, that bypasses some parts of a circuit. A short circuit can occur when two bare wires in a circuit meet each other. The circuit bypassed by the short circuit stops to function, and a large amount of current might start to flow. This may produce a lot of heat in the wires and start a fire. As a safety action, circuit breakers and fuses automatically open the circuit to stop an excessive current. There are two types of circuits known as series and parallel circuits.
In a series circuit, we have the same current flows through all the elements. The entire voltage and resistance across the circuit is the sum of the voltage and resistance across each part of the system. In this type of the circuit, R = R_1 + R_2 + R_3 and V = V_1 + V_2 + V_3 . A well-known example of a series circuit is a chain of Christmas lights, and if any one of the bulbs is missed or burned out, there will be no current flow, and none of the lights will work.
Parallel circuits are similar to the smaller blood veins that branch off from an artery and then join in a vessel to return blood to the heart. Now imagine two wires, each as an artery and a vein, that are connected to each other with some smaller wires. These smaller wires have the same voltages applied to them, but different amounts of current flow through them based on the individual wires’ resistance.
A simple example of a parallel circuit is the wiring system in a house. A single electric source supplies all the appliances and lights with the same voltage, and if one of the bulbs burns out, the current can still pass through the rest of the devices and lights. It should be mentioned that if there is a short circuit in the system, the voltage will drop to nearly zero, and the whole system goes down.
Circuits are frequently very complex combinations of series and parallel circuits.
What are Electrical Circuits and Their Types?
We can connect two-terminal components and Electrical networks in series or parallel. These resulting electrical networks will have two terminals and can operate in a parallel or series topology. Whether a two-terminal device is an electrical component (just a resistor) or an electrical network (resistors in series) is a matter of viewpoint. We can name a “component” as two-terminal objects that are gathered in the series/parallel networks.
Components combined in series are connected in a single electrical path. Each component has the same current through the path, equal to the current in the network. The voltage in the network is equivalent to the sum of the voltages in each component.
Components in a parallel configuration are connected with multiple paths, and each element has the same voltage, equal to the voltage over the network. The current in the network is equivalent to the sum of the currents of each component.
The two introducing statements are the same for the series and the parallel circuits, except for replacing the voltage and current role. Many circuits can be named as a combination of series and parallel circuits, along with other arrangements.
In series circuits, the current flowing through each of the elements is the same. The voltage across the circuit is the total amount of the individual voltage drops in all the components. In parallel circuits, the voltage in each of the elements is the same, and the entire current is the total amount of the currents flowing through all the components.
Considering a very simple circuit including four light bulbs and a 12-volt battery, If the battery joins to one bulb with a wire and to the next bulbs in a row until reaching back to the battery, we have one continuous loop, and the bulbs are assumed to be in series. If all bulbs are wired to the battery in a separate loop, they are said to be in parallel. The same current flows through all of the bulbs in the series circuits, and the voltage is 3-volts for each bulb, which may not be enough to make them emit light. If we have these light bulbs connected in parallel, the light bulbs’ currents combine to make the current in the battery. In this configuration, the voltage drop is 12-volts over all the bulbs, and they will all glow.
In series circuits, all the components must function for the circuit to be operative. The entire circuit is broken if one bulb burns out in a series circuit. In a parallel circuit, every light bulb has its own circuit and loop, so by incomplete wires in each light bulb, and the last one will still emit light.
Series Configuration Circuit
First, an example of a series circuit:
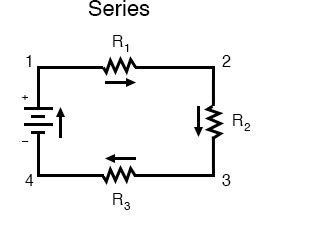
Here, there are three resistors (labeled as R1, R2, and R3) connected in a long string from one head of the battery to the other end. It should be noted that the subscript labeling(those little numbers to the lower-right of each letter “R”) are irrelevant to the resistance values in ohms. They attend only to identify one resistor from another.
The defining feature of a series circuit is that there is just one path for current to flow. The current flows in a clockwise direction in the presented circuit, from point 1 to point 2, 3, 4, and back to the first position 1.
Parallel Circuit Configuration
Let’s look at the parallel type of circuit. A parallel configuration diagram is presented below:
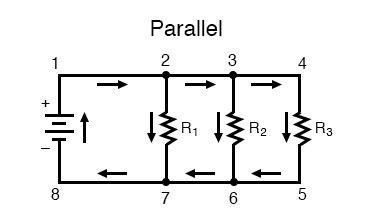
Same as the previous one, we have three resistors here, but this time they make more than one connected path for current to flow. There is one path for 1 to 2 to 7 to 8 and all back to 1 again. There is another path from 1 to 2 to 3 to 6 to 7 to 8 and again back to 1. Then, we have a third one from 1 to 2 to 3 to 4 to 5 to 6 to 7 to 8 and again back to 1. Each path (within R1, R2, and R3) is named a branch.
A parallel circuit’s defining characteristic is that all components are connected to the same set of electrically same points. Looking at the presented diagram, we can see that all the points 1, 2, 3, and 4 are electrically common, as well as points 8, 7, 6, and 5, which are the same too. All resistors and the battery are connected to these two sets of points.
The complexity of a circuit does not stop at an easy series and parallel wiring! We can have a combination of series and parallel circuits too.
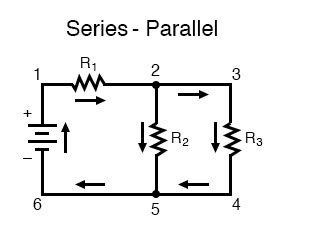
Series-Parallel Configuration Circuit
A combination of series and parallel may be a complex circuit needing much time for design and analysis. In this type of circuit illustrated below, there are two loops for the current to flow: one path from 1 to 2, 5, 6 and back to 1 again, and another from 1 to 2, 3, 4, 5, 6 and back to 1 again. Just notice how both currents pass through R1 (in the path of point 1 to point 2). In the presented configuration, R2 and R3 are in parallel with each other, and R1 is in series with the parallel compound of R2 and R3.
Resistors in Series and Parallel
Fundamentally, resistors limit the flow of current and charge in a circuit and an ohmic device. Most circuits possess more than one resistor in the system. Suppose several resistors have many connections and all connected to a battery. In this case, the battery’s current is based on the equivalent resistance of the circuit.
The equivalent resistance of a compound of resistors depends on both their particular ohmic values and how they are connected in the system. The simplest combinations of resistors are parallel and series connections, as discussed before. For review, the output current of the first resistor flows into the second resistor’s input In series circuits; therefore, the current is the same in all resistors. In a parallel circuit, all of the resistors are connected together on both heads. Each resistor has an equal potential drop in a parallel configuration, and the currents passing each resistor may be different, depending on the resistor’s ohmic value. The sum of all the currents equals the current flowing in the parallel connections.
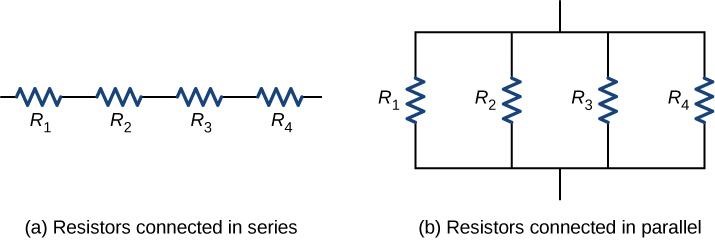
Circuits of simple series and parallel resistors. (a) For a series of resistors, the current is the same in each resistor. (b) For a parallel connection for resistors, the voltage across each resistor is the same. (Reference: openpress.usask.ca)
Resistors in Series
Resistors are called to be in series whenever the current passes through the resistors sequentially. Consider the figure below, which shows three resistors in a row with an applied voltage equal to Vab. As there is only one connection for the charges to flow, each resistor’s current is the same. The equivalent resistance of a series of resistors in a lineup connection is equal to the individual resistances’ algebraic sum.
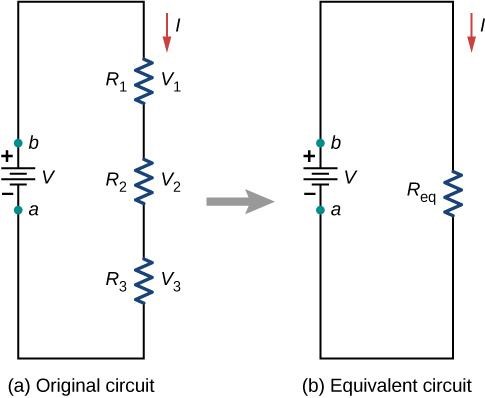
The coming current from the voltage source passes through each resistor, so each resistor’s current is the same. The current in the circuit is based on the voltage supplied by the voltage source and the resistors’ resistance. For each resistor, a potential drop V occurs that is equal to electric potential energy loss as a current passes through each resistor. Based on Ohm’s law, the potential drop across resistors when a current flows through them is calculated employing the equation V=IR, where I is the current in amps (A), and R is the element’s resistance in ohms ( \Omega ). As energy is conserved, and the voltage is the potential energy per charge, the sum of the voltage in the circuit by the source and the potential drops over the resistors in a loop must be zero:
\sum_{i=1}^{N}V_i=0
This equation is often mentioned as Kirchhoff’s loop law, and you will read it in more detail in this article. For the presented loop, the sum of the potential drops for each resistor and the voltage provided by the voltage source (battery) should equal to zero:
V-V_1-V_2-V_3=0
V=V_1+V_2+V_3
V=IR_1+IR_2+IR_3
I=\frac{V}{R_1+R_2+R_3}=\frac{V}{R_eq}
By considering the current through each component equal, we can explain the equality by an equivalent resistance, which is just the sum of the individual resistors’ resistances.
Several numbers of resistors can be connected in series. Considering N resistor in these series, the equivalent resistance is:
R_eq= R_1+R_2+R_3+...=\sum_{i=1}^{N}R_i
One outcome of components connected in a series circuit is affecting all the other components by turning off one component. For example, if many lamps are connected in series, and one light burns out, all the other bulbs go dark.
Strategy for Calculations
In a series circuit, an equivalent resistance is the algebraic equation sum of the resistances as mentioned in the last section. The current in the circuit is calculated using Ohm’s law and is equal to the equation of the V=IR. The potential drop in each of the resistors can be calculated using Ohm’s law and using each resistor. The power consumed by each resistor can be obtained using P=RI^{2} . The resistors’ total power dissipation is equal to the sum of the power consumed by each resistor. The power provided by the battery can be determined using P=I\varepsilon .
Capacitors in Series and Parallel
Many capacitors can be connected to each other to be operative in various applications. Several connections of capacitors function as a single equivalent capacitor. This equivalent single capacitor’s total capacitance value is based on both individual capacitors and how they are connected. Capacitors can be arrayed in two simple and common sorts of connections, named series and parallel. These two basic compounds, series and parallel, can also be utilized as a part of more complex connections in larger systems.
The Series Combination of Capacitors
The figure below presents a series of combinations of three capacitors arranged in a line inside a closed circuit. As for any capacitor, the combination’s capacitance is related to the charge and voltage using Equation C=\frac{Q}{V} . By connecting this series combination to a battery (voltage supply) with voltage V, each capacitor will acquire an identical charge. First, to explain, the charge on the plates connected to the battery’s positive terminal is Q, and the charge on the plates connected to the negative terminal is -Q. Charges affect the other plates, and the sum of the charges on all plates, and also the sum of charges on each pair of capacitor plates, is equal to zero. Although, the potential drop V_1=Q/C_1 of one capacitor may not be the same as the potential drop V_1=Q/C_1 on another capacitor as the capacitors generally have different capacitances. A series of two or three capacitors makes a single capacitor with lower capacitance. Any number of capacitors joined in series generally is equivalent to one capacitor with a capacitance (named the equivalent capacitance) smaller than the smallest capacitances in the combination. Charge in this equivalent capacitor is equal to the charge on each of the capacitors in series combinations, which means all capacitors in a series circuit have the same charge. This equality happens due to the conservation of charge in the system.
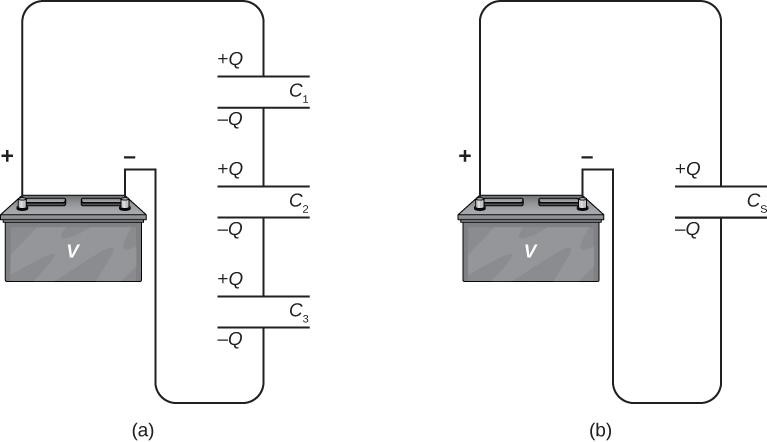
We can calculate an expression for the equivalent capacitance by finding the voltages across each capacitor. The potentials in capacitors 1, 2, and 3 are V_1=Q/C_1, V_2=Q/C_2 , and V_3=Q/C_3 , respectively. We must sum up these potentials to find the voltage of the battery by using the following potential balance:
V=V_1+V_2+V_3
Potential V is measured in an equivalent capacitor that has a charge of Q and an equivalent capacitance C. Entering these expressions for V_1, V_2, and V_3 gives us this equation:
\frac{Q}{C_S}=\frac{Q}{C_1}+\frac{Q}{C_2}+\frac{Q}{C_3}
Canceling the charge Q, presents an expression for the equivalent capacitance, C_s containing three series capacitors connected:
\frac{1}{C_S}=\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}
This equation can be generalized to several capacitors in a series network.
\frac{1}{C_S}=\sum_{i=1}^{N}\frac{1}{C_i}
The Parallel Combination of Capacitors
A parallel combination using three capacitors is illustrated in the figure below. This combination has one plate of each capacitor in one point connected to one side of the circuit, and the other plates join to the other side. As the capacitors are connected parallelly, they all have the same voltage V in their plates. Each capacitor in this parallel network may have a different charge. For finding the equivalent capacitance C_P in the parallel network, we should say that the total charge Q in the network is the sum of all the all charges:
Q=Q_1+Q_2+Q_3
We use the relation Q=C_PV On the left-hand side of this equation, which is the charge for the entire network. Also, we can use the relations Q_1=C_1V , Q_2=C_2V, and Q_3=C_3V for each capacitor in the network and the right-hand side of the equation. In this way, we have:
C_PV=C_1V+C_2V+C_3V
By simplified this equation, the expression for the equivalent capacitance in the parallel network of tree capacitors is:
C_P=C_1+C_2+C_3
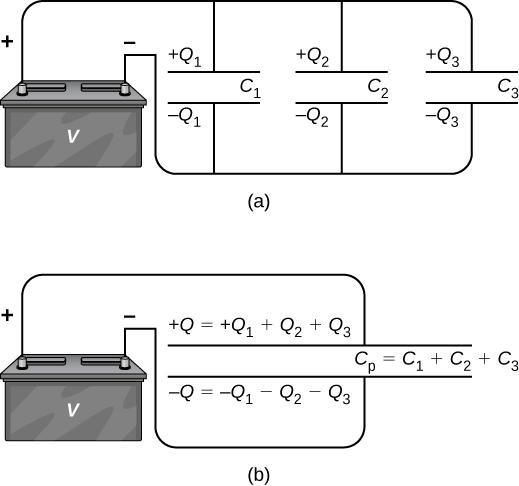
This expression can easily generalized for any number of capacitors connected in a parallel network:
C_P=\sum_{i=1}^{N}C_i
Buy Equipment or Ask for a Service
By using Linquip RFQ Service, you can expect to receive quotations from various suppliers across multiple industries and regions.
Click Here to Request a Quotation From Suppliers and Service Providers
Read More on Linquip