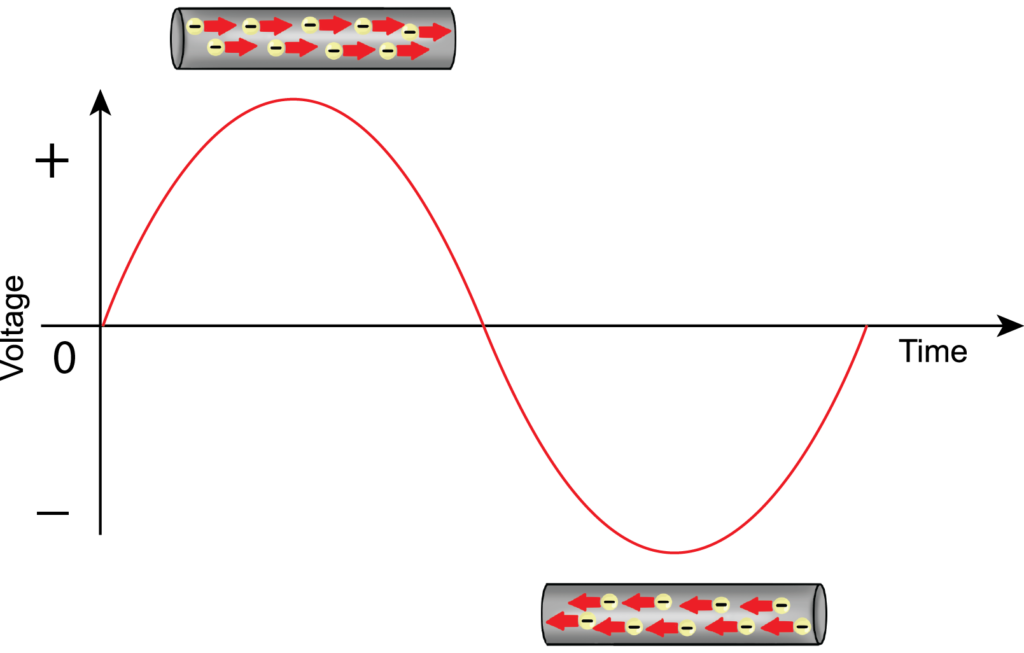
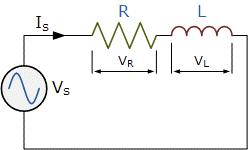AC Circuit: Application, Types and Characteristics

Table of Contents

Alternating Current Circuits or AC circuits are simply circuits powered by an Alternating Source, either current or voltage. An Alternating Voltage or Current is one in which the amount of either the voltage or the current alters about a distinct mean value and reverses direction periodically.

In an ac circuit, the source voltage and current have a phase angle, which may be calculated by dividing the resistance by the impedance. The phase angle has an impact on the average power provided to an RLC circuit. Several Suppliers and Companies, as well as other manufacturers and distributors, supply various Ac devices, and there are numerous AC Devices for Sale on Linquip.

There is a comprehensive list of AC device services on the Linquip website that covers all OEM fleets. Linquip vendors can assist you with this. Please call AC Device Experts in Linquip to learn more about how to connect with a diverse group of service providers who consistently deliver high-quality products.

Most household and industrial systems and Appliances in the present-day are powered using alternating current. All DC-based plugged-in rechargeable battery-based devices technically operate based on an alternating current. DC devices all utilize DC power obtained from AC for charging their powering system and batteries.

The alternating circuit was made for the first time in the 1980s when Tesla aimed to solve the numerous incapability of Thomas Edison’s DC generators. He attempted to present a way of transferring electricity at a high voltage. Then, by employing transformers to step it up or down for distribution, we would be able to minimize power loss across long distances, which was the center of Direct Current’s problems at the time.

Direct Current Vs Alternating Current (AC vs DC)

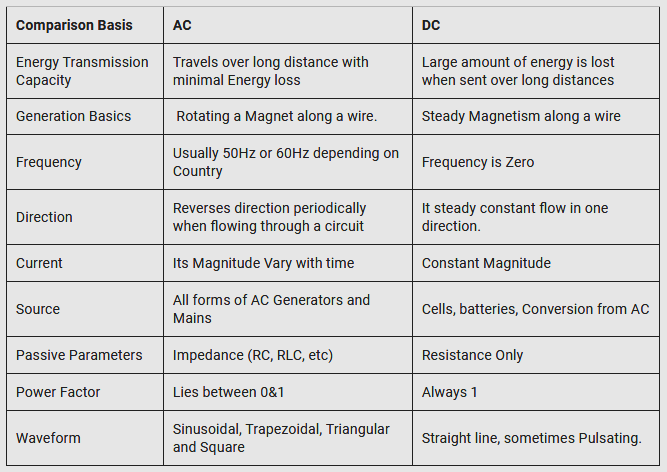
AC and DC differ in many ways from transmission to generation and distribution. The significant difference between the DC and AC, which is also the basis of their diverse characteristics, is the direction of the flow of electricity. In DC, electrons flow continuously in a specific direction or forward, but in the AC system, electrons exchange their direction of movement in periodic intervals. This alternating current also leads to alternation of the voltage value as it changes along from negative to positive in line with the current.

What is an AC circuit?

Electrical and electronic circuits include many different connecting components to form a closed and complete circuit. The main passive components employed in any circuit are Capacitor, Resistor , and Inductor. All three of named passive components have one feature in common; they limit the electrical current in a circuit but totally in very various ways.

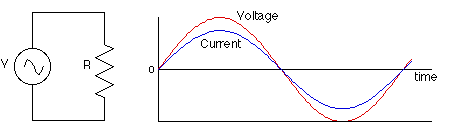
18 What is AC Circuit Reference physics.bu .edu ac circuit — What is AC Circuit Reference **physics.bu.edu**

Electrical current can pass through a circuit in two ways. If it passes in one single direction only, it is named Direct Current (DC). If the electrical current alternates in divers directions back and forth, it is named Alternating Current (AC). As they offer an impedance inside a circuit, passive components in AC circuits act quite differently compared to those in DC circuits.

Passive components in the circuit consume electrical energy. Therefore, they can not amplify or increase the power of any electrical signals applied to them. Simply it is all because they are passive and will always have a gain of less. Passive components placed in an electrical and electronic circuit can be combined in an infinite number of designs, as shown below, with the performance of these circuits based on the interaction between their various electrical properties.

How Do You Analyze an Electric Circuit?

Ohm’s Law is the most significant law in circuit analysis. Voltage=Resistance*Current (V=IR) indicates that the voltage across an element is equal to the element’s current times the current flowing through the element. The quantity of electric potential measured in volts is called voltage (V).

What are Reactant and Impedance?

The type of circuits, which the current is proportional to the voltage are named linear circuits. In a resistor, The ratio of voltage to current is its resistance. Resistance does not have the independence to the frequency, and they have two phases. Still, circuits with only resistors are not very exciting and applicable.

Generally, frequency does not affect the ratio of voltage to current, and there is a phase difference. So the general name for the ratio of voltage to current is impedance. The symbol of the impedance is Z. Resistance is a particular case of impedance. Another special example is that the current and voltage are out of phase by 90°; this is an essential case because there is no power loss in the circuit when this occurs. In this case, where the current and voltage are out of phase by 90°, we name reactance as the ratio of voltage to current, and its symbol is X.

Terminology

For compression, we shall indicate electrical potential difference as voltage. We will consider voltages and currents as a function that varies sinusoidally with time and use lower case i and v for the current and voltage when explicitly analyzing their variation. We shall represent the amplitude or peak value of the sinusoidal variation by Vm and I_m, while V = V_m/√2 and I = I_m/√2 with no subscripts refer to their RMS values. To understand the source of the sinusoidally varying voltage and how we use them, see this post.

The voltage and the current we use in AC can be presented as the following equations:

$v = v(t) = V_m sin( \omega t )$

$i = i(t) = I_m sin( \omega t +\varphi )$

where:

\omega

= 2πf = the angular frequency

f = the ordinary or cyclic frequency = the number of complete oscillations per second.

\varphi

= the phase difference between the voltage and current.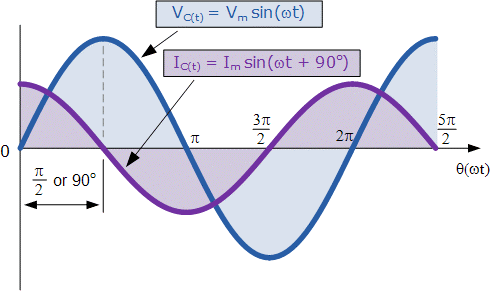

Passive Components in AC Circuits

We can name R as resistance, C as capacitance, and L as inductance. Whether we use resistors in DC or AC circuits, they always have the same value of resistance in the system no matter what is the supply frequency. It is all because resistors are identified to be pure, having parasitic characteristics such as zero inductance L = 0 and infinite capacitance C = ∞. Also, for a fully resistive circuit, we always have an in-phase voltage and current, so we can find the power consumed at any instant by multiplying the voltage by the current.

On the other hand, capacitors and inductors have a distinct type of AC resistance known as reactance, as mentioned before (X_L and X_C). Reactance also blocks the current flow, but the value of reactance is not a fixed amount for one capacitor or inductor compared to a resistor with a fixed value of resistance. The reactance quantity for an inductor or a capacitor is based on the frequency of the supply current and the DC value of the element itself.

Also, there is a commonly used list of passive components in AC circuits and their corresponding equations that can be applied to find their impedance and reactance value of circuit current. It should be mentioned that here we presented a theoretically perfect (pure) inductor or capacitor that does not have any resistance. But in the real world, we always have a combination of the components mentioned earlier, which includes resistance as well.

Fully Resistive Circuit

Resistors impede, regulate, or set the flow of current in a distinct path or impose a voltage cut in an electrical circuit base on this current flow. Resistors have a sort of impedance called resistance ( R ). The resistive quantity of a resistor is measured in Ohms, Ω, and can be found either in a fixed value or a shifting value (potentiometers).

Impedance and current value can be found using the following equations:

$Z=\frac{V_R}{I_R}=R$

$Z=\angle 0^{\circ} = R+J0$

$I_S=\frac{V_S}{R}$

Fully Capacitive Circuit

The capacitor is a component that has the capacity and can save energy in the shape of an electrical charge, the same as a small battery. The capacitance quantity of a capacitor is measured in Farads (F), and at the DC circuit, a capacitor has an infinite impedance (open-circuit). On the other hand, a capacitor has zero impedance (short-circuit) at very high frequencies. Impedance and current value can be found using the following equations:

$X_C =\frac{V_C}{I_C}=\frac{1}{2\pi fC}$

$Z=\angle -90^{\circ}=0-jX_C$

$I_S= \frac{V_S}{X_S}$

Fully Inductive Circuit

An inductor includes a coil of wire that induces a magnetic field within itself or a central core due to the current flowing through the coil. The inductance quantity of an inductor is measured in the Henries unit (H). At DC circuits, an inductor is a short-circuit and has zero impedance. In contrast, at high frequencies, an inductor has an infinite impedance (open-circuit). Impedance and current value can be found using the following equations:

$X_L =\frac{V_L}{I_L}=2\pi fL$

$Z=\angle 90^{\circ}=0+jX_C$

$I_S= \frac{V_S}{X_L}$

Series AC Circuits

We can connect passive components together in series combinations in AC circuits to form RC, RL, and LC circuits, as explained below.

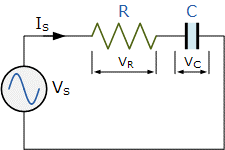
Series RC Circuit

The circuit and the equation for the series RC circuit are:

$Z= \sqrt{R^{2}+X_C^{2}}$

$Z=\angle -\phi = R-jX_C$

$\phi (90\rightarrow 0) = tan^{-1}(-\frac{X_C}{R})$

$I_S= \frac{V_S}{\sqrt{R^{2}+X_C^{2}}}$

$V_S=\sqrt{V_R^{2}+V_C^{2}}$

Series RL Circuit

The circuit diagram and the equation for the series RL circuit are:

$Z= \sqrt{R^{2}+X_L^{2}}$

$Z=\angle \phi = R+jX_C$

$\phi (90\rightarrow 0) = tan^{-1}(\frac{X_L}{R})$

$I_S= \frac{V_S}{\sqrt{R^{2}+X_L^{2}}}$

$V_S=\sqrt{V_R^{2}+V_L^{2}}$

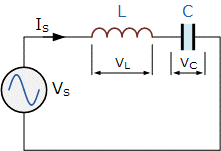
Series LC Circuit

The circuit diagram and the equation for the series LC circuit are:

$Z=\sqrt{(X_C-X_L)^{2}}$

$\therefore Z= X_C-X_L or X_L-X_C$

$Z=\angle (\phi _1+\phi _2)= 0 + jX_L-jX_C$

$f_r=\frac{1}{2\pi \sqrt{LC}}$

$I_S=I_L=I_C$

Parallel AC Circuits

We can connect passive components together in series combinations in AC circuits to form RC, RL and LC circuits, as explained below.

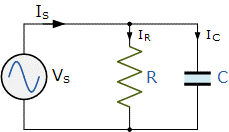
Parallel RC Circuit

The circuit diagram and the equation for the parallel RC circuit are:

$I_R=\frac{V_s}{R}, I_C=\frac{V_S}{X_C}$

$I_S=\sqrt{I_R^{2}+I_C^{2}}$

$\phi = tan^{-1}(\frac{I_C}{I_R})$

$Y= \frac{1}{Z}=\sqrt{G^{2}+B_c^{2}}$

$V_S=V_C=V_R$

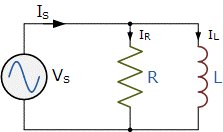
Parallel RL Circuit

The circuit diagram and the equation for the parallel RL circuit are:

$I_L=\frac{V_s}{R}, I_C=\frac{V_S}{X_L}$

$I_S=\sqrt{I_R^{2}+I_L^{2}}$

$\phi = tan^{-1}(\frac{I_L}{I_R})$

$Y= \frac{1}{Z}=\sqrt{G^{2}+B_L^{2}}$

$V_S=V_L=V_R$

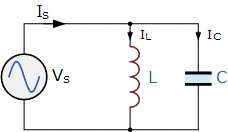
Parallel LC Circuit

The circuit diagram and the equation for the parallel LC circuit are:

$B_L=\frac{1}{X_L}, B_C=\frac{1}{X_C}$

$Y=\frac{1}{Z}=B_L+B_C$

$f_R=\frac{1}{2\pi \sqrt{LC}}$

$V_S=V_L=V_C$

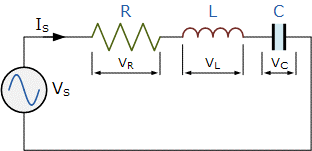
RLC Circuits

We can connect all three passive components in an AC circuit, both series and parallel RLC combinations, as explained below.

Series RLC Circuit

The circuit diagram and the equation for the series RLC circuit are:

$Z= \sqrt{R^{2}+(X_C-X_l)^{2}}$

$Z=\angle \phi =R+jX$

$V_S=\sqrt{V_R^{2}+(V_C-V_L)^{2})}$

$I_S=\frac{V_s}{Z}=\frac{V_S}{\sqrt{R^{2}+(X_C-X_l)^{2}}}$

$\phi = tan^{-1}(\frac{X_L-X_C}{R})$

$I_S=I_R=I_C=I_L$

Parallel RLC Circuit

The circuit diagram and the equation for the parallel RLC circuit are:

$G=\frac{1}{R}, B_L=\frac{1}{X_L} ,B_C=\frac{1}{X_C}$

$Y=\frac{1}{Z}=\sqrt{G^{2}+(B_l-B_C)^{2}}$

$I_S=\sqrt{I_R^{2}+(I_L-I-C)^{2}}$

$f_R=\frac{1}{2\pi\sqrt{LC}}$

$V_S=V_C=V_R=V_L$

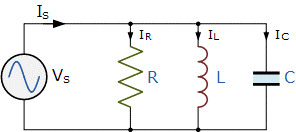
It has shown above in AC circuits that passive components behave very differently than when employed in a DC circuit due to the presence of frequency ( ƒ ). In a fully resistive circuit, we have in-phase current and voltage. In a fully capacitive circuit, the current in the capacitor has -90^o with the voltage, while it is 90^o for a fully inductive circuit.

In series circuits, the phasor sum of the voltages across the circuit components is equivalent to the supply voltage (V_S). On the other hand, In a parallel circuit, the phasor sum of the flowing currents in each element is equal to the supply current (I_S).

For both series and parallel connection of the RLC circuits, resonance occurs at XL = XC when the source current is “in-phase” with the circuit’s supply voltage. A Series Circuit Resonance is identified as an Acceptor Circuit, and a Parallel Resonance Circuit is identified as a Rejecter Circuit.

Power in AC Circuit

In DC circuits, the power of the components is simply the output of the DC voltage times the current in watts. However, for an AC circuit with reactive elements, we have to assess the consumed power differently.

Electrical power is the energy consumed in a circuit. All the electrical and electronic elements and devices have a limitation for the amount of electrical energy they can safely handle. For instance, we have a 1/4 watt resistor or a 20-watt amplifier.

The amount of power in circuits at any moment is called instantaneous power and is known by the famous relationship of power equals amps times volts (P = VI). As a result, one watt will be equal to the volt-ampere result of one-volt times one-ampere (one watt is the rate of consuming energy at one joule per second).

So, the power consumed or provided by a circuit element is the voltage across the element and the current flowing within it. Suppose we have a resistance of “R” ohms in a DC circuit. In that case, the power dissipated in watts is given by any of the following generalized equations:

$P=V\times I=R\times I^{2}=\frac{V^{2}}{R}$

where:

V: DC voltage

I: DC current

R: Resistance value.

Electrical Power in an AC Circuit

In DC circuits, the voltages and currents are constant and do not vary with time as there is no sinusoidal waveform function related to the supply. In contrast, the instantaneous values of the current, voltage, and resulted power in an AC circuit are continually changing by the supply. Therefore, we are not able to calculate the power in AC circuits the same as the previous method. However, we can still assume that power is equal to the amperes (i) times the voltage (v).

Another critical point is that AC circuits have reactance, so the components create magnetic and/or electric fields. Unlike a purely resistive element, The power is deposited and then returned back to the circuit as the sinusoidal waveform passes in one complete periodic cycle.

As a result, the average power consumed by a circuit is the sum of the energy stored and the power returned in one complete cycle. A circuit’s average power consumption is the average instantaneous power during one full cycle. The instantaneous power (p) can be defined as the instantaneous voltage (v) times the instantaneous current (i).

By assuming the sinusoidal waveforms of the voltage and current, we have:

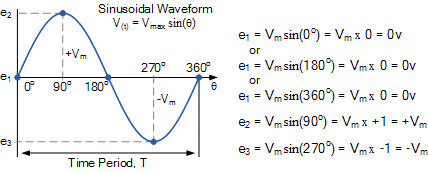
$P=v\times i$

$V=V_msin(\omega t+\phi _v)$

$i=I_msin(\omega t+\phi _i)$

$p= [V_msin(\omega t+\theta _v)\times I_msin(\omega t+\theta _i)]$

$\therefore V_mI_m(sin(\omega t+\theta _i)\times sin(\omega t+\theta _v) )$

The trigonometric product-to-sum is:

$sin(A+B)=\frac{1}{2}[cos(A-B)-cos(A+B)]$

Where $\theta =\theta _v-\theta _i$ , and by placing in the above equation we have:

$p=\frac{V_mI_m}{2})(cos(\theta )-cos(2\omega t+\theta ))$

$\frac{V_mI_m}{2}=\frac{V_m}{\sqrt{2}}\times \frac{I_m}{\sqrt{2}}=V_{RMS}\times I_{RMS}$

where V_RMS and I_RMS are the root-mean-squared values of the sinusoidal waveforms of the v and i, respectively. Therefore we can display the instantaneous power as:

$P=VIcos\theta - cos(2\omega t+\theta ))$

This equation shows us that the instantaneous AC power includes two different parts and is the sum of two terms. The second part is a sinusoidal function of time with a frequency of twice the angular frequency of the supply. However, the first term is a constant whose value is based on the phase difference, θ between the voltage and the current.

As the instantaneous power is continually varying with the sinusoid function over time, it is hard to measure. Therefore, it is more convenient and simple to employ the mean value or average of the power. So the average value of the instantaneous power is given simply as the following equation over a certain number of cycles:

$p=V\times I\times cos(\theta )$

The AC Power consumed in a circuit can also be calculated by using the impedance (Z) of the circuit as presented below:

$Z=\sqrt{R^{2}+(X_L-X_C)^{2}}$

$\theta =cos^{-1}\frac{R}{Z}=sin^{-1}\frac{X_L}{Z}=tan^{-1}\frac{X_L}{R}$

$\therefore p=\frac{V^{2}}{Z}cos\theta =I^{2}Zcos\theta$