The steam turbine efficiency can be defined as the ratio of the turbine useful output energy to the energy to which it is delivered. Energy loss in various forms, such as heat or friction, prevents the steam turbine from being 100% efficient.
Various elements that determine the efficiency of a steam turbine include: thermodynamic (temperature and steam pressure) and hydraulic (inlet fluid velocity) parameters, guide vanes angle, rotor blades angle, and rotor diameter.
The thermodynamic efficiency of multistage (moderate to high-pressure ratio) steam turbines ranges from 65 percent for very small (under 1,000 kW) units to over 90 percent for big industrial and utility-sized units. Small, single-stage steam turbines can have as low as 40% efficiency. Steam Turbine Efficiency is an important aspect of Choosing This Product to use in industrial applications. Steam Turbines are provided by several Suppliers and Companies, different manufacturers, and a lot of distributors and there are a lot of Steam Turbines for Sale on Linquip.
Linquip’s website has a complete selection of Steam Turbines Services that will meet all of your needs. Linquip can connect you with a number of Steam Turbine service providers and professionals. Linquip offers a team of Steam Turbine and subject matter specialists who can help you test your equipment.
In the following parts, the basis of steam turbine operation is briefly introduced. Then, we will explain the method of calculating the steam turbine efficiency.
Steam Turbine
The steam turbine is a type of turbine that converts the potential energy of heated and compressed steam, generated in a steam generator or steam of natural origin like from geothermal sources, into kinetic energy by steam expansion in the turbine blades and consequently into mechanical work on the rotating shaft. The transmission of power between the steam and the rows of rotary blades mounted on the turbine rotor changes the total steam enthalpy.
The steam turbine is used as a section of stationary and transport steam turbine power plants. Besides turbine units, the power plants include boilers as the units to generate steam, steam condensers, and other equipment.
Why Is Steam Turbine Efficiency So Low?
Because of two factors, the total Steam Turbine Efficiency is fairly low (about 29%). For starters, a significant quantity of heat is lost in the condenser, and heat losses also occur at other points throughout the plant. It is impossible to avoid heat loss in the condenser.
Which Is More Efficient Gas or Steam Turbine?
The steam turbine’s relatively basic design makes it more efficient to maintain. For industrial steam turbines, a steam turbine may achieve up to 90% efficiency, and occasionally even more. As a result, steam turbines are the most efficient in most applications.
Principle of Operation
An ideal steam turbine is supposed to undergo an isentropic process or a procedure with constant entropy. So, during this process, the entering steam entropy is equal to the left steam entropy. But, as is predicted, there is no isentropic steam turbine. The steam turbine isentropic efficiencies range typically from 20% to 90%, according to the application of the turbine.
The inside of a steam turbine contains several sets of blades. A group of stationary blades is attached to the casing, and the other set of rotary blades is connected to the shaft. These sets are designed, and the clearances are determined so that the turbine has the maximum utilization of steam expansion.
The thermal efficiency of practical steam turbines varies with turbine capacity, load, and physical losses. It can reach values up to about 50% in a 1200 MW turbine; As the turbine goes smaller in size, they have lower efficiencies.
To maximize turbine efficiency, the steam turbine structure comprises a number of stages. In each stage, the energy is extracted, and they are known as impulse or reaction turbines. Most steam turbines employ a combination of impulse and reaction designs. Although each stage works as either one or the other, the entire turbine utilizes both of them. In most cases, lower pressure parts are of reaction type, and higher pressure stages are impulse turbines.
The following figure shows the complete cycle of different units of a steam turbine. The steam is superheated before entering the turbine unit.
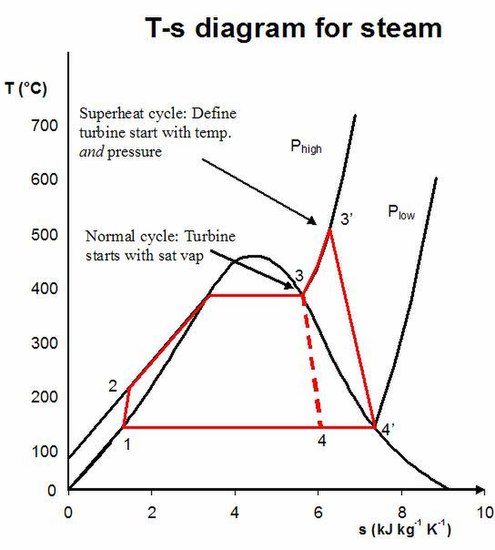
The steam turbine works in parts 3-4 of the Rankine cycle based on thermodynamics principles (above figure). Superheated steam enters the turbine after leaving the boiler at high temperature and pressure. Then, the steam kinetic energy increases when passing through a fixed nozzle in an impulse type turbine or the fixed vanes in a reaction turbine. The high-velocity steam leaves the nozzle towards the turbine rotor blades.
A force is applied on the blades due to the vapor pressure and causes the rotor to spin. A generator or other similar device can be installed on the shaft to store and use the energy that was in the steam. After the turbine, steam reaches the condenser to be cooled in the form of saturated vapor or a mix of liquid and vapor at a lower temperature and pressure than what entered into the turbine.
By applying the first law of thermodynamics, we can attain an equation for calculating the work produced per unit mass. With the assumption of not existing heat transfer to the surrounding environment and neglecting the changes in kinetic and potential energy compared to the change in specific enthalpy, we can write the following formula:
\frac{\dot{W}}{\dot{m}}=h_3-h_4
h3 and h4 are the steam enthalpy in the entrance and exit of the turbine unit, respectively. Also, Ẇ and ṁ are the rate of work developed by the turbine per time unit and the flow rate, respectively.
Steam Turbine Efficiency
This section will introduce the steam turbine efficiency under two types of impulse and reaction turbines.
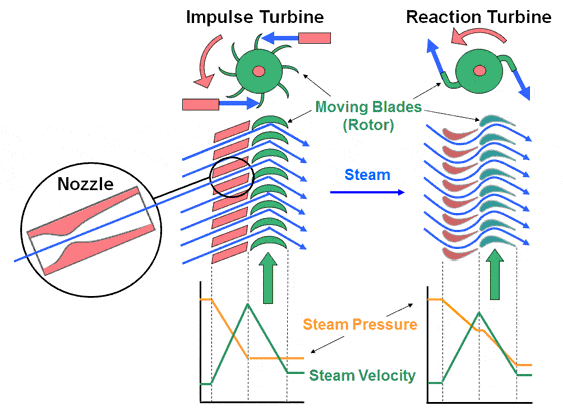
Impulse Turbine
Fixed nozzles in an impulse turbine lead the steam flow into high-speed jets with significant kinetic energy. As the steam jet changes direction with striking the bucket-like shaped rotor blades, the kinetic energy is converted into shaft rotation. A pressure drop happens only over the stationary blades, along with an increase in net steam velocity across the stage. Through the nozzle, the pressure falls. Due to the high expansion ratio of steam, the outgoing steam through the nozzle has a very high velocity.
The law of moment of momentum asserts that the sum of the moments of applied external forces on a fluid is equivalent to the net time variation of angular momentum flux.
F_u=\dot{m}\mathit{\Delta}V_w
In the above equation, Fu is the tangential force on the blade, and ΔVw is the difference between the inlet and outlet tangential velocities.
\mathit{\Delta}V_w=V_{w1}-V_{w2}
The work developed by the turbine is:
W=\dot{m}U\mathit{\Delta}V_w
U is the blade speed and is calculated as below:
U=\omega r
ω and r are the turbine angular velocity and radius, respectively.
Blade Efficiency
Blade efficiency is defined by the ratio of the work done on the blades to kinetic energy provided to the fluid.
{\eta }_b=\frac{U\mathit{\Delta}V_w}{V^2_1}
Here, V1 is the absolute inlet velocity.
Stage Efficiency
In an impulse turbine, a stage consists of a set of the nozzle and a moving wheel. The stage efficiency is defined as the ratio of work done in the stage to the enthalpy drop in the nozzle.
{\eta }_{stage}=\frac{U\mathit{\Delta}V_w}{\mathit{\Delta}h}
\mathit{\Delta}h=h_2-h_1
The last equation gives the specific enthalpy drop in the nozzle. From the first law of thermodynamics:
h_1+\frac{1}{2}V^2_1=h_2+\frac{1}{2}V^2_2
So, assuming V1 is very small,
\mathit{\Delta}h=\frac{1}{2}V^2_2
Moreover, stage efficiency is calculated by the following relation:
{\eta }_{stage}={\eta }_b{\eta }_N
ηN is nozzle efficiency and given by:
{\eta }_N=\frac{V^2_2}{2\left(h_1-h_2\right)}
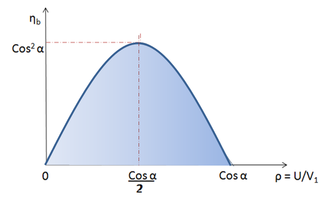
It can be shown that maximum stage efficiency is gained if we put the following ratio in the expression of blade efficiency:
\frac{U}{V_1}=\frac{1}{2}cos\alpha
where α is the guide vane angle.
So,
{\eta }_{b,max}=\frac{1}{2}\alpha \ \left(1+\frac{V_{r2}}{V_{r1}}\right)\
Vr1 and Vr2 show relative velocities at inlet and outlet, respectively. By neglecting blade surface friction, we have:
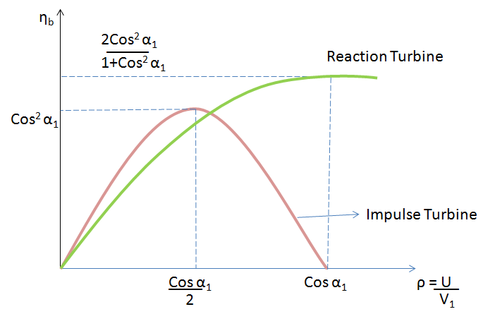
{\eta }_{b,max}=\alpha \
It means that, as α rises, the work done on the blades decreases. However, due to the reduction in surface area of the blade, there are less frictional losses.
Reaction Turbine
A reaction turbine rotor blades are designed to form convergent nozzles. A reaction turbine uses the reaction force with the acceleration of steam through the nozzles. Steam is directed to the rotor by the stationary guide vanes. It leaves the stationary part as a jet filling the entire periphery of the rotor. The steam then turns direction and its speed relative to the speed of the blades increases.
The steam experiences a pressure drop within both the stator and the rotor when it accelerates within the first and decelerates in the latter. No net change occurs in steam velocity through the stage, but it has a decrease in both pressure and temperature, which means work is done in the rotor motion.
Blade Efficiency
The energy provided to blades is:
E=\mathit{\Delta}h
and
{\mathit{\Delta}}_h=\mathit{\Delta}h_f+\mathit{\Delta}h_m
The first and second terms in the above equation right-hand side refer to enthalpy drop through the fixed and moving blades, respectively.
The inlet steam velocity in the nozzle is very small. So,
\mathit{\Delta}h_f=\frac{V^2_!}{2}
Also,
\mathit{\Delta}h_m=\frac{V^2_{r2}-V^2_{r1}}{2}
Therefore,
E=\frac{V^2_1}{2}+\frac{V^2_{r2}-V^2_{r1}}{2}
It can be shown that the blade efficiency is calculated by the following equation:
\eta_{b}=\frac{2U(2V_{1}cos \alpha-U)}{2V_{1}^{2}-U^{2}+2V_{1}cos\alpha}
It is also shown by mathematical operations that the maximum blade efficiency of the reaction turbine can be calculated as follows:
{\eta }_{b,max}=\frac{2\alpha \ }{1+\alpha \ }
The following figure compares the efficiency of impulse and reaction turbines.
Isentropic Efficiency
To estimate how well a turbine is operating, we can use the isentropic steam turbine efficiency. This parameter measures the similarity of the turbine in real working conditions with the turbine with ideal conditions that are assumed to be isentropic.
When calculating this isentropic steam turbine efficiency, the heat lost to the surroundings is considered zero. The turbine entrance pressure and temperature are the same for both the actual and the isentropic turbines.
However, at the turbine exit, the steam specific enthalpy for the real turbine is more than that for the ideal turbine. This is due to irreversibility in the actual conditions. To give a good comparison between the two cases, the steam specific enthalpy is estimated at the same pressure for the actual and ideal turbines.
The following equation is used to find the isentropic steam turbine efficiency based on the T-s diagram of a steam power plant, available as the first figure of the present article.
\eta =\frac{h_3-h_4}{h_3-h_{4s}}
The indices represent the thermodynamic states seen in the mentioned diagram. The s index also represents the isentropic turbine.
Download Steam Turbine Efficiency PDF
Read More In Linquip
- Easy Guide to Cooling Tower Efficiency & How To Increase it
- Transformer Efficiency: Essential Things You Should Know
- How to Calculate the Efficiency of Heat Exchangers?
- Top 10 Steam Turbine Manufacturers in USA in 2022
- Top 10 Steam Turbine Manufacturers in World (2022 Update)
- Top Steam Turbine Manufacturers in India in 2022
- The 7 Best Steam Generators in 2022
- Steam Condenser: Basics, Parts, Advantages and Disadvantages
- The Practical Guide To The Difference Between Gas Turbine and Steam Turbines
- How Does a Steam Turbine Work? A Simple Descriptive Guide
- Types of Steam Turbine: An easy-to-understand and practical Classification
- Steam Turbine Parts: A Comprehensive and understandable Introduction to All Components




Nice material to us