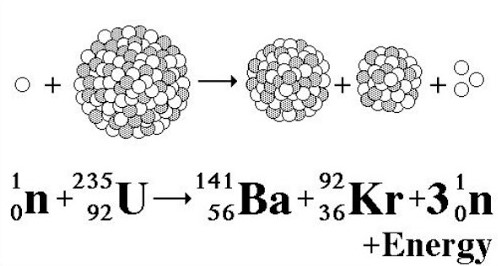
Nuclear Fission Equation – Nuclear fission is a reaction in which a nucleus is split. Controlled fission is a fact whereas controlled fusion is a dream that may be reached in the future. Hundreds of nuclear fission power plants worldwide attest that controlled fission is possible and economical. Global warming has caused nuclear power as a viable and attractive energy alternative to fossil fuels.
Linquip’s website provides all of the information about nuclear equipment and devices you could need. Linquip’s team of experts is ready to answer any questions you may have about nuclear fission. The best place to start learning about nuclear equipment is Linquip’s article, “What Is Nuclear Power?“.
Discover a range of nuclear devices & equipment with Linquip’s Nuclear Products list. You can also sign up to become a Linquip Expert and take advantage of all the service’s features. Have you ever been interested in Guest Posting on Linquip? You can submit your content as a guest on the Linquip platform.
About 440 nuclear power reactors generate around 10% of the world’s electricity. According to the World Nuclear Association, about 50 more reactors are under development, equivalent to around 15% of the current capacity. In 2019 nuclear plants provided 2657 TWh of electricity, up from 2563 TWh in 2018. France produces over 75% of its electricity with nuclear power, while the US has 104 running reactors giving 20% of its electricity.
Nuclear Fission Basics
As mentioned before, fission is the splitting of a nucleus that delivers free neutrons and lighter nuclei. The fission of heavy particles is extremely exothermic than burning coal, releasing about 200 million eV. The quantity of energy discharged during nuclear fission is millions of times more effective per mass than that of coal, assuming that only 0.1 percent of the original nuclei is transformed into energy.
In the 1930s, scientists determined that some nuclear reactions can be launched and regulated. Scientists ordinarily performed this task by blasting a large isotope with a second, smaller one — usually a neutron. The collision made the larger isotope break apart into two or more components called nuclear fission. The following equation is the nuclear fission of uranium-235:
_{92}^{235}\textrm{U}+_{0}^{1}\textrm{n}\rightarrow_{56}^{142}\textrm{Ba}+_{36}^{91}\textrm{Kr}+3_{0}^{1}\textrm{n}
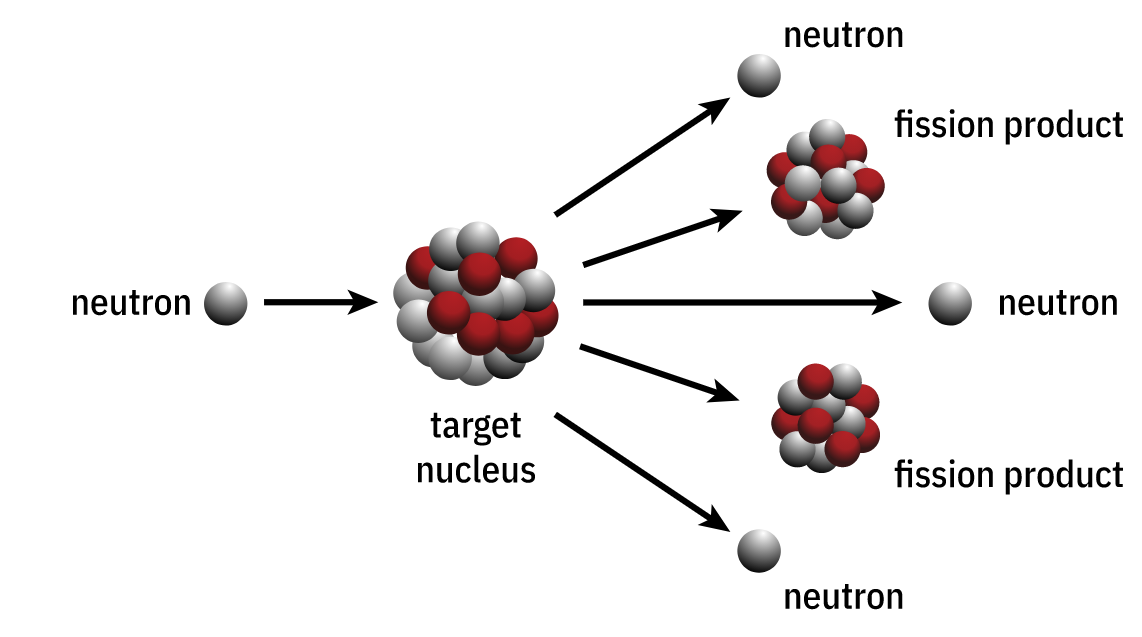
The mentioned equation is not unique. Let us clarify this problem. Statistical probability governs the number of neutrons and the specific fission products from any fission event. In that, the exact break-up of a single nucleus cannot be foretold.
Nevertheless, conservation laws need the total number of nucleons and the total energy to be conserved. The fission reaction in U-235 creates fission products such as Ba, Kr, Sr, Cs, I, and Xe, as shown in the above equation, with atomic masses distributed around 95 and 135. Here are some other examples of typical reaction products along with the released energy:
U-235+n\rightarrow \rightarrow Ba-144+Kr-90+2n+about~200~MeV
U-235+n\rightarrow \rightarrow Ba-141+Kr-92+3n+about~170~MeV
U-235+n\rightarrow \rightarrow Zr-94+Te-139+3n+about~197~MeV
In the mentioned equations, the number of nucleons (protons + neutrons) is conserved, as shown in the following relations for the above equations:
235 + 1 = 144 + 90 + 2,
235 + 1 = 141 + 92 + 3,
235 + 1 = 94 + 139 + 3.
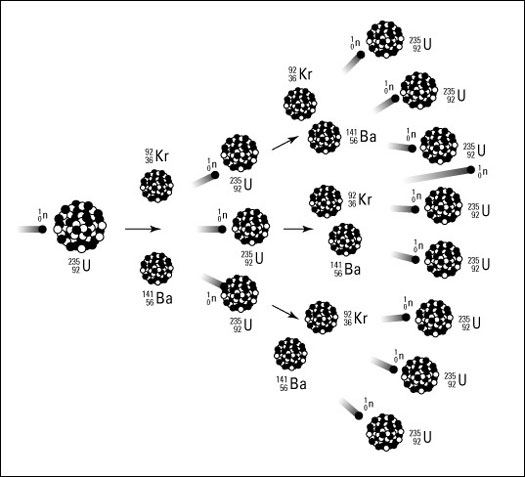
However, a slight loss in atomic mass may be determined, which is equivalent to the energy discharged. The barium and krypton isotopes consequently decay and form more stable neodymium and yttrium isotopes, with numerous electrons’ emissions from the nucleus (beta decays). The beta decay, with remarkably associated gamma rays, makes the fission products extremely radioactive. This radioactivity diminishes with time. The following figure depicts an illustration of the chain reaction:
To determine the energy discharged during the mass loss in nuclear fission, we apply Einstein’s equation that relates energy and mass:
E=mC^{2}
Critical Mass
The blast of a bomb only happens if the chain reaction passes its critical mass. The critical mass is the limit at which a chain reaction converts to self-sustaining. If the neutrons are dropped faster than they are produced by fission, the reaction is not self-sustaining. The spontaneous nuclear fission rate is the incident per second that produces atom fission spontaneously, without any external interference.
In nuclear power plants, nuclear fission is managed by a medium such as water in the nuclear reactor. The water serves as a heat transfer environment to cool down the reactor and slow down neutron particles. By this procedure, the neutron emission and usage are controlled. If the nuclear reaction is not controlled because of a lack of cooling water, then a meltdown occurs.
Examples of Nuclear Fission Equations
In this section, we are going to solve two examples of the Nuclear Fission Equation to clarify this topic more.
Example One
Calculate the amount of energy released for the fission reaction of the 235U when 144Cs and 90Rb are two neutrons.
So, let’s first write the balance equation:
_{92}^{235}\textrm{U}+_{0}^{1}\textrm{n}\rightarrow _{55}^{144}\textrm{Cs}+_{37}^{90}\textrm{Rb}+2_{0}^{1}\textrm{n}
The strategy for solving such problems is summarized below:
- First, calculate the change in the mass in the reaction, then convert this mass to the energy change per atom.
- Then the change in mass per mol of U-235 should be calculated. Then the energy shift can be calculated.
Let’s take a look at the solution to this problem.
The change in mass follows the reaction can be calculated using the following relations:
\Delta m=\mathrm{mass_{products}}-\mathrm{mass_{reactants}}=\textrm{mass}(_{55}^{144}\textrm{Cs}+\,_{37}^{90}\textrm{Rb}+\,_0^1\textrm n)-\textrm{mass }\,_{92}^{235}\textrm U
=(143.932077\textrm{ amu}+89.914802\textrm{ amu}+1.008665\textrm{ amu})-\textrm{235.043930 amu}
=-0.188386\textrm{ amu}
So, the energy variation in electronvolts per atom is:
\Delta E=(-0.188386\textrm{ amu})(931\textrm{ MeV/amu})=-175\textrm{ MeV}
The difference in mass per mole of _{92}^{235}\textrm{U} is -0.188386~g = -0.188386\times 10^{-4} kg, so the shift in energy in kilojoules per mole is:
\Delta E=(\Delta m)c^2=(-1.88386\times10^{-4}\textrm{ kg})(2.998\times10^8\textrm{ m/s})^2
=-1.693\times10^{13}\textrm{ J/mol}=-1.693\times10^{10}\textrm{ kJ/mol}
Example Two
Suppose we are going to determine the energy discharged in the following fission reaction:
_{}^{238}\textrm{U}\rightarrow _{}^{95}\textrm{Sr}+_{}^{140}\textrm{Xe}+3_{}^{}\textrm{n}
Like the previous example, the energy discharged is equivalent to the mass consumed times c2, so we need to find the mass variation within the parent 238U and the fission products. The total mass of products is:
m_{products}=94.919388~u + 139.921610~u + 3(1.008665)~u=237.866993~u
So, the mass lost is:
\Delta m=238.050784 ~u-237.8669933 ~u=0.183791~u
Finally, the energy released can be calculated using the following equation:
E=(\Delta m)C^{2}
= (0.183791~u)\frac{931.5~MeV/C^{2}}{u}C^{2}=171.2~MeV
What Is the Purpose of Nuclear Fission?
Fission generates energy for nuclear power and supplies nuclear weapons. Several substances called nuclear fuels can be used for both purposes because, when hit by fission neutrons, they undergo fission and emit neutrons when they break apart.
Download Nuclear Fission Equation PDF
To make this article accessible to you at any time, we have made it a PDF document.
Buy Equipment or Ask for a Service
By using Linquip RFQ Service, you can expect to receive quotations from various suppliers across multiple industries and regions.
Click Here to Request a Quotation From Suppliers and Service Providers
Read More on Linquip
- Nuclear Fission Equation With Example
- What are the Disadvantages of Nuclear Fusion?
- How Does Nuclear Fusion Work?
- Differences Between Nuclear Fusion and Fission
- Types of Nuclear Reactors: Differences and Operation Principles
- EMF Equation of Transformer- Turns Voltage Transformation Ratio of Transformer